Spiky cubes, Pac-Man walking, empty M&M’s chocolate: curse of dimensionality
“Curse of dimensionality” means the difficulties of machine learning which arise when the dimension of data is higher. In short if the data have too many features like “weight,” “height,” “width,” “strength,” “temperature”…. that can undermine the performances of machine learning. The fact might be contrary to your image which you get from the terms “big” data or “deep” learning. You might assume that the more hints you have, the better the performances of machine learning are. There are some reasons for curse of dimensionality, and in this article I am going to introduce three major reasons below.
- High dimensional data usually have rich expressiveness, but usually training data are too poor for that.
- The behaviors of data points in high dimensional space are totally different from our common sense.
- More irrelevant featreus lead to confusions in recognition or decision making.
Through these topics, you will see that you always have to think about which features to use considering the number of data points.
1, Number of samples and degree of dimension
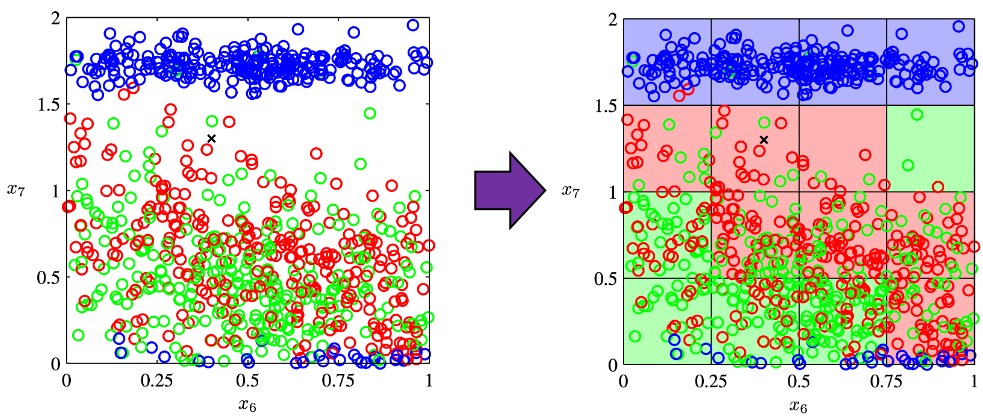
The most straightforward demerit of adding many features, or increasing dimensions of data, is the growth of computational costs. More importantly, however, you always have to think about the degree of dimensions in relation of the number of data points you have. Let me take a simple example in a book “Pattern Recognition and Machine Learning” by C. M. Bishop (PRML). This is an example of measurements of a pipeline. The figure below shows a comparison plot of 3 classes (red, green and blue), with parameter x7 plotted against parameter x6 out of 12 parameters.
* The meaning of data is not important in this article. If you are interested please refer to the appendix in PRML.
Assume that we are interested in classifying the cross in black into one of the three classes. One of the most naive ideas of this classification is dividing the graph into grids and labeling each grid depending on the number of samples in the classes (which are colored at the right side of the figure). And you can classify the test sample, the cross in black, into the class of the grid where the test sample is in.
As I mentioned the figure above only two features out of 12 features in total. When the the total number of plots is fixed, and you add remaining ten axes one after another, what would happen? Let’s see what “adding axes” mean. If you are talking about 1, 2, or 3 dimensional grids, you can visualize them. And as you can see from the figure below, if you make each ![]() grids respectively in 1, 2, 3 dimensional spaces, the number of the small regions in the grids are respectively 10, 100, 1000. Even though you cannot visualize it anymore, you can make grids for more than 3 dimensional data. If you continue increasing the degree of dimension, the number of grids increases exponentially, and that can soon surpass the number of training data points soon. That means there would be a lot of empty spaces in such high dimensional grids. And the classifying method above: coloring each grid and classifying unknown samples depending on the colors of the grids, does not work out anymore because there would be a lot of empty grids.
grids respectively in 1, 2, 3 dimensional spaces, the number of the small regions in the grids are respectively 10, 100, 1000. Even though you cannot visualize it anymore, you can make grids for more than 3 dimensional data. If you continue increasing the degree of dimension, the number of grids increases exponentially, and that can soon surpass the number of training data points soon. That means there would be a lot of empty spaces in such high dimensional grids. And the classifying method above: coloring each grid and classifying unknown samples depending on the colors of the grids, does not work out anymore because there would be a lot of empty grids.
* If you are still puzzled by the idea of “more than 3 dimensional grids,” you should not think too much about that now. It is enough if you can get some understandings on high dimensional data after reading the whole article of this.
I said the method above is the most naive way, but other classical classification methods , for example k-nearest neighbors algorithm, are more or less base on a similar idea. Many of classical machine learning algorithms are based on the idea smoothness prior, or local constancy prior. In short in classical ways, you do not expect data to change so much in a small region, so you can expect unknown samples to be similar to data in vicinity. But that soon turns out to be problematic when the dimension of data is bigger because you will not have training data in vicinity. Plus, in high dimensional data, you cannot necessarily approximate new samples with the data in vicinity. The ideas of “close,” “nearby,” or “vicinity” get more obscure in high dimensional data. That point is related to the next topic: the intuition have cultivated in normal life is not applicable to higher dimensional data.
2, Bizarre characteristics of high dimensional data
We form our sense of recognition in 3-dimensional way in our normal life. Even though we can visualize only 1, 2, 3 dimensional data, we can actually expand the ideas in 2 or 3 dimensional sense to higher dimensions. For example 4 dimensional cubes, 100 dimensional spheres, or orthogonality in 255 dimensional space. Again, you cannot exactly visualize those ideas, and for many people, such high dimensional phenomenon are just imaginary matters on blackboards.
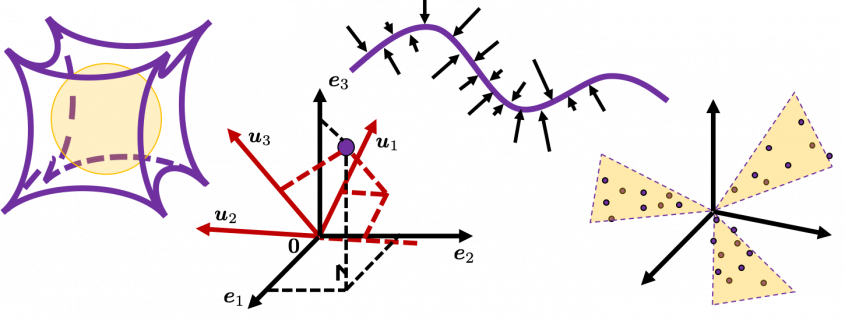
Those high dimensional ideas are designed to retain some conditions in 1, 2, or 3 dimensional space. Let’s take an example of spheres in several dimensional spaces. One general condition of spheres, or to be exact the surfaces of spheres, are they are a set of points, whose distance from the center point are all the same.
For example you can calculate the value of a D-ball, a sphere with radius ![]() in
in ![]() dimensional space as below.
dimensional space as below. 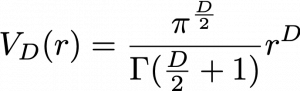
Of course when ![]() is bigger than 3, you cannot visualize such sphere anymore, but you define such D-ball if you generalize the some features of sphere to higher dimensional space.
is bigger than 3, you cannot visualize such sphere anymore, but you define such D-ball if you generalize the some features of sphere to higher dimensional space.
Just in case you are not so familiar with linear algebra, geometry, or the idea of high dimensional space, let’s see what D-ball means concretely.
But there is one severe problem: the behaviors of data in high dimensional field is quite different from those in two or three dimensional space. To be concrete, in high dimensional field, cubes are spiky, you have to move like Pac-Man, and M & M’s Chocolate looks empty inside but tastes normal.
2_1: spiky cubes
Let’s look take an elementary-school-level example of geometry first.
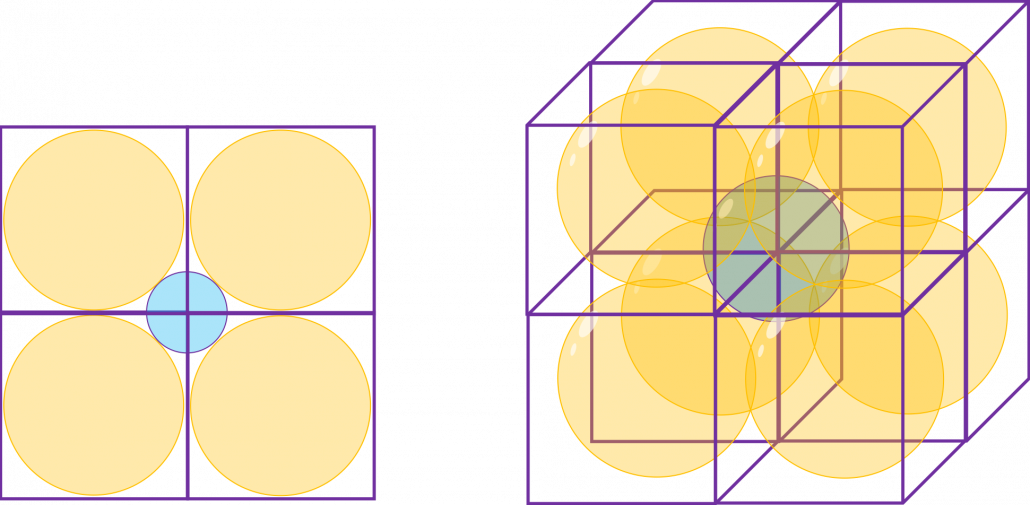
In the first section, I wrote about grids in several dimensions. “Grids” in that case are the same as “hypercubes.” Hypercubes mean generalized grids or cubes in high dimensional space.
* You can confirm that the higher the dimension is the more spiky hypercube becomes, by comparing the volume of the hypercube and the volume of the D-ball inscribed inside the hypercube. Thereby it can be proved that the volume of hypercube concentrates on the corners of the hypercube. Plus, as I mentioned the longest diagonal distance of hypercube gets longer as dimension degree increases. That is why hypercube is said to be spiky. For mathematical proof, please check the Exercise 1.19 of PRML.
2_2: Pac-Man walking
Next intriguing phenomenon in high dimensional field is that most of pairs of vectors in high dimensional space are orthogonal. First of all, let’s see a general meaning of orthogonality of vectors in high dimensional space.
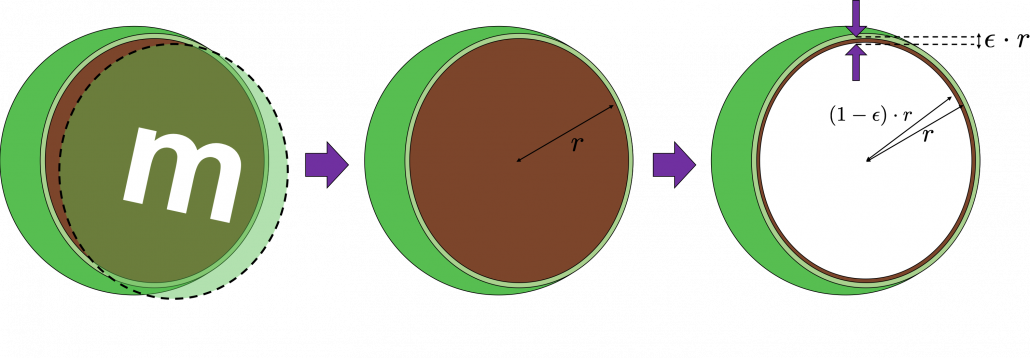
2_3: empty M & M’s chocolate
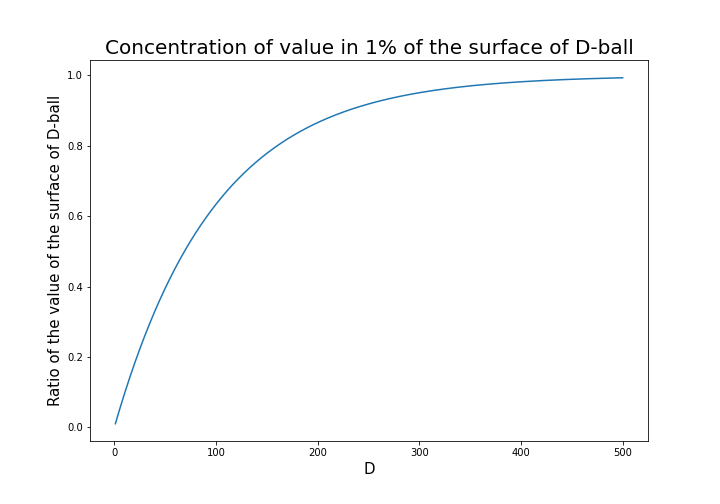
That is why, in high dimensional space, M & M’s chocolate look empty but tastes normal: all the chocolate are concentrated beneath the sugar coating. Of course this is also contrary to our daily sense, and inside M & M’s chocolate is a mysterious world.
This fact is especially problematic because many machine learning algorithms depends on distances between pairs of data points. Even if you van approximate the distance between two points as zero, like you do in ////, there is no guarantee that you can do the same thing in higher dimensional
3, Peeking phenomenon






Leave a Reply
Want to join the discussion?Feel free to contribute!