Statistics – Page 2 – Data Science Blog

Statistical Relational Learning – Part 2

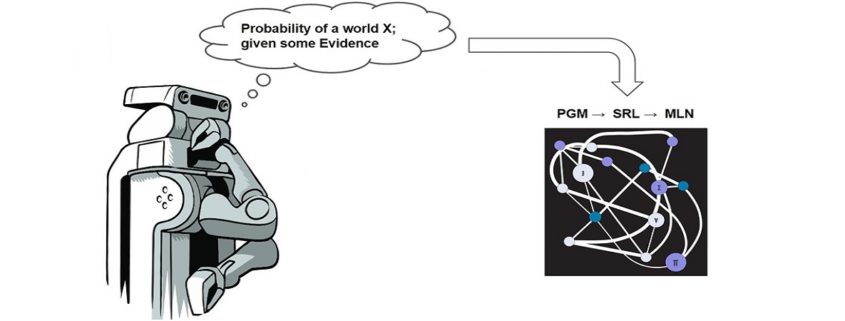
January 18, 2017/4 Comments/in Artificial Intelligence, Data Mining, Data Science, Data Science at the Command Line, Machine Learning, Statistics, Tools, Tutorial /by Vishal Bhalla

In the first part of this series on “An Introduction to Statistical Relational Learning”, I touched upon the basic Machine Learning paradigms, some background and intuition of the concepts and concluded with how the MLN template looks like. In this blog, we will dive in to get an in depth knowledge on the MLN template; again with the help of sample examples. I would then conclude by highlighting the various toolkit available and some of its differentiating features.

MLN Template – explained

A Markov logic network can be thought of as a group of formulas incorporating first-order logic and also tied with a weight. But what exactly does this weight signify?

Weight Learning

According to the definition, it is the log odds between a world where F is true and a world where F is false,

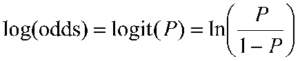
and captures the marginal distribution of the corresponding predicate.

Each formula can be associated with some weight value, that is a positive or negative real number. The higher the value of weight, the stronger the constraint represented by the formula. In contrast to classical logic, all worlds (i.e., Herbrand Interpretations) are possible with a certain probability [1]. The main idea behind this is that the probability of a world increases as the number of formulas it violates decreases.

Markov logic networks with its probabilistic approach combined to logic posit that a world is less likely if it violates formulas unlike in pure logic where a world is false if it violates even a single formula. Consider the case when a formula with high weight i.e. more significance is violated implying that it is less likely in occurrence.

Another important concept during the first phase of Weight Learning while applying an MLN template is “Grounding”. Grounding means to replace each variable/function in predicate with constants from the domain.

Weight Learning – An Example

Note: All examples are highlighted in the Alchemy MLN format

Let us consider an example where we want to identify the relationship between 2 different types of verb-noun pairs i.e noun subject and direct object.

The input predicateFormula.mln file contains

The predicates nsubj(verb, subject) and dobj(verb, object) and
Formula of nsubj(+ver, +s) and dobj(+ver, +o)

These predicates or rules are to learn all possible SVO combinations i.e. what is the probability of a Subject-Verb-Object combination. The + sign ensures a cross product between the domains and learns all combinations. The training database consists of the nsubj and dobj tuples i.e. relations is the evidence used to learn the weights.

When we run the above command for this set of rules against the training evidence, we learn the weights as here:

Note that the formula is now grounded by all occurrences of nsubj and dobj tuples from the training database or evidence and the weights are attached to it at the start of each such combination.

But it should be noted that there is no network yet and this is just a set of weighted first-order logic formulas. The MLN template we created so far will generate Markov networks from all of our ground formulas. Internally, it is represented as a factor graph.where each ground formula is a factor and all the ground predicates found in the ground formula are linked to the factor.

Inference

The definition goes as follows:

Estimate probability distribution encoded by a graphical model, for a given data (or observation).

Out of the many Inference algorithms, the two major ones are MAP & Marginal Inference. For example, in a MAP Inference we find the most likely state of world given evidence, where y is the query and x is the evidence.

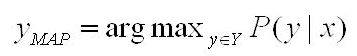
which is in turn equivalent to this formula.

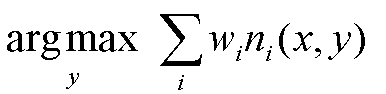
Another is the Marginal Inference which computes the conditional probability of query predicates, given some evidence. Some advanced inference algorithms are Loopy Belief Propagation, Walk-SAT, MC-SAT, etc.

The probability of a world is given by the weighted sum of all true groundings of a formula i under an exponential function, divided by the partition function Z i.e. equivalent to the sum of the values of all possible assignments. The partition function acts a normalization constant to get the probability values between 0 and 1.

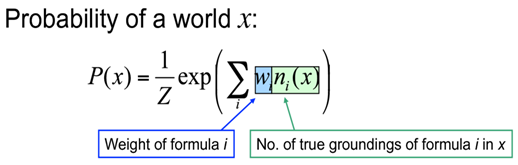
Inference – An Example

Let us draw inference on the the same example as earlier.

After learning the weights we run inference (with or without partial evidence) and query the relations of interest (nsubj here), to get inferred values.

Tool-kits

Let’s look at some of the MLN tool-kits at disposal to do learning and large scale inference. I have tried to make an assorted list of all tools here and tried to highlight some of its main features & problems.

For example, BUGS i.e. Bayesian Logic uses a Swift Compiler but is Not relational! ProbLog has a Python wrapper and is based on Horn clauses but has No Learning feature. These tools were invented in the initial days, much before the present day MLN looks like.

ProbCog developed at Technical University of Munich (TUM) & the AI Lab at Bremen covers not just MLN but also Bayesian Logic Networks (BLNs), Bayesian Networks & ProLog. In fact, it is now GUI based. Thebeast gives a shell to analyze & inspect model feature weights & missing features.

Alchemy from University of Washington (UoW) was the 1st First Order (FO) probabilistic logic toolkit. RockIt from University of Mannheim has an online & rest based interface and uses only Conjunctive Normal Forms (CNF) i.e. And-Or format in its formulas.

Tuffy scales this up by using a Relational Database Management System (RDBMS) whereas Felix allows Large Scale inference! Elementary makes use of secondary storage and Deep Dive is the current state of the art. All of these tools are part of the HAZY project group at Stanford University.

Lastly, LoMRF i.e. Logical Markov Random Field (MRF) is Scala based and has a feature to analyse different hypothesis by comparing the difference in .mln files!

Hope you enjoyed the read. The content starts from basic concepts and ends up highlighting key tools. In the final part of this 3 part blog series I would explain an application scenario and highlight the active research and industry players. Any feedback as a comment below or through a message is more than welcome!

Back to Part I – Statistical Relational Learning

Additional Links:

[1] Knowledge base files in Logical Markov Random Fields (LoMRF)

[2] (still) nothing clever Posts categorized “Machine Learning” – Markov Logic Networks

[3] A gentle introduction to statistical relational learning: maths, code, and examples

Wahrscheinlichkeitsverteilungen – Zentralen Grenzwertsatz verstehen mit Pyhton

December 15, 2016/0 Comments/in Business Analytics, Data Mining, Data Science, Data Science Hack, Python, Python, Statistics, Tutorial /by Benjamin Aunkofer

Wahrscheinlichkeitsverteilung sind im Data Science ein wichtiges Handwerkszeug. Während in der Mathevorlesung die Dynamik dieser Verteilungen nur durch wildes Tafelgekritzel schwierig erlebbar zu machen ist, können wir mit Programmierkenntnissen (in diesem Fall wieder mit Python) eine kleine Testumgebung für solche Verteilungen erstellen, um ein Gefühl dafür zu entwickeln, wie unterschiedlich diese auf verschiedene Wahrscheinlichkeitswerte, Varianz und Mengen an Datenpunkten reagieren und wann sie untereinander annäherungsweise ersetzbar sind – der zentrale Grenzwertsatz. Den Schwerpunkt lege ich in diesem Artikel auf die Binominal- und Normalverteilung.

Für die folgenden Beispiele werden folgende Python-Bibliotheken benötigt:

1

2

3

import matplotlib.pyplot as pyplot

import random as random

import math as math

R Data Frames meistern mit dplyr – Teil 1

November 21, 2016/2 Comments/in Data Mining, Data Science, Data Science Hack, R Statistics, Statistics, Tutorial /by Dr. Uwe Schneider

Dieser Artikel ist Teil 1 von 2 aus der Artikelserie R Data Frames meistern mit dplyr.

Data Frames sind das Arbeitspferd von R, wenn Daten in eine Struktur gepackt werden sollen, um sie einzulesen, zu säubern, zu transformieren, zu analysieren und zu visualisieren. Abstrakt gesprochen sind Data Frames nichts anderes als Relationen, also Mengen von Tupels, gebildet aus Elementen von geeigneten Mengen.

Dieses Konzept hat sich auch außerhalb des R-Universums bestens bewährt, umzusammengesetzte Daten, Beobachtungen oder Geschäftsobjekte zu repräsentieren. Der beste Beleg für diese Aussage sind die allgegenwärtigen Relationalen Datenbanksysteme (RDBMS). Dort werden Relationen als Tabellen (Tables) oder Sichten (Views) bezeichnet, und darauf wirkt eine mächtige, imperative Abfrage- und Manipulationssprache namens Structured Query Language, kurz:
SQL.

SQL ist in meiner Wahrnehmung die Lingua Franca der Datenverarbeitung, da sie im Kern über sehr viele Softwareprodukte gleich ist und nach erstaunlich geringem Lernaufwand mächtige Auswerte- und Manipulationsoperationen an den Daten ermöglicht. Hier eine SQL-Anweisung, um eine fiktive Tabelle aller Verkäufe (SALES) nach den Top-10-Kunden in diesem Jahr zu untersuchen:

1

2

3

4

5

6

7

SELECT customer_id, SUM(sales_amt) AS amount,

COUNT(*) AS n_sales, COUNT(DISTINCT product_id) AS n_products

FROM sales

WHERE sales_date LIKE ’2016-%’

GROUP BY customer_id

ORDER BY SUM(sales_amt) DESC

LIMIT 10

Dieser selbsterklärliche Code aus sieben Zeilen hat einen enormen Effekt: Er fast alle Verkäufe des Jahres 2016 auf Basis der Kundennummer zusammen, berechnet dabei die Summe aller Verkaufsbeträge, zählt die Anzahl der Transaktionen und der verschiedenen vom Kunden gekauften Produkte. Nach Sortierung gemäß absteigenden Umsatzes schneidet der Code nach dem 10. Kunden ab.

SQL kann aber mit der gleichen Eleganz noch viel mehr: Beispielsweise verbinden Joins die Daten mehrerer Tabellen über Fremschlüsselbeziehungen oder analytische Funktionen bestimmen Rankings und laufende Summen. Wäre es nicht toll, wenn R ähnlich effektiv mit Data Frames analoger Struktur umgehen könnte? Natürlich! Aber schon der Versuch, obige SQL-Query auf einem R Data Frame mit den althergebrachten Bordmitteln umzusetzen (subset, aggregate, merge, …), führt zu einem unleserlichen, uneleganten Stück Code.

Genau in diese Bresche springt der von vielen anderen Bibliotheken bekannte Entwickler Hadley Wickham mit seiner Bibliothek dplyr: Sie standardisiert Operationen auf Data Frames analog zu SQL-Operationen und führt zu einer wirklich selbsterklärlichen Syntax, die noch dazu sehr performant abgearbeitet wird. Ganz analog zu ggplot2, das sich an der Grammar of Graphics orientiert, spricht Wickham bei dplyr von einer Grammar of Data Manipulation. Die Funktionen zur Manipulation nennt er folgerichtig Verben.

Dabei treten naturgemäß eine Reihe von Analogien zwischen den Teilen eines SELECT-Statements und dplyr-Funktionen auf:

SELECT-Operation	dplyr-Funktion
Bildung der Spaltenliste	select()
Bildung eines Ausdrucks	mutate()
WHERE-Klausel	filter()
GROUP BY Spaltenliste	group_by()
Bildung von Aggregaten wie sum() etc.	summarise()
HAVING-Klausel	filter()
ORDER BY Spaltenliste	arrange()
LIMIT-Klausel	slice()

Die ersten Schritte

Ich möchte die Anwendung von dplyr mithilfe des Standard-Datensatzes Cars93
aus dem Paket MASS demonstrieren:

1

2

3

4

5

6

7

> install.packages("dplyr")

> library(dplyr)

> cars <- MASS::Cars93

> str(cars)

’data.frame’: 93 obs. of 27 variables:

$ Manufacturer : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 ...

$ Model : Factor w/ 93 levels "100","190E","240",..: 49 56 ...

Die erste Aufgabe soll darin bestehen, aus dem Data Frame alle Autos zu selektieren, die vom Hersteller “Audi” stammen und nur Model und Anzahl Passagiere auszugeben. Hier die Lösung in Standard-R und mit dplyr:

1

2

3

4

5

6

7

8

9

10

11

> # Standard R: Zu allen Audis das Model, Anzahl Insassen

> subset(cars,Manufacturer=="Audi")[,c("Model","Passengers")]

Model Passengers

3 90 5

4 100 6

>

> # Das gleiche mit dplyr

> select(filter(cars,Manufacturer=="Audi"),Model,Passengers)

Model Passengers

1 90 5

2 100 6

Man sieht, dass die neue Funktion filter() der Zeilenselektion, also der Funktion subset() entspricht. Und die Auswahl der Ergebnisspalten, die in Standard-R durch Angabe einer Spaltenliste zwischen [ und ] erfolgt, hat in dplyr das Pendant in der Funktion select().

select() ist sehr mächtig in seinen Möglichkeiten, die Spaltenliste anzugeben. Beispielsweise funktioniert dies über Positionslisten, Namensmuster und ggf. das auch noch negiert:

1 2	select(cars, -starts_with("L"))

Die obige Abfrage projiziert aus dem Data Frame sämtliche Spalten, die nicht mit “L” beginnen. Das scheint zunächst ein unscheinbares Feature zu sein, zahlt sich aber aus, wenn analytische Data Frames Dutzende oder Hunderte von Spalten haben, deren Bezeichnung sich nach einem logischen Namensschema richtet.
Soweit ist das noch nicht spektakulär. dplyr hilft uns in obigem Beispiel, als erstes bestimmte Datensätze zu selektieren und als zweites die interessierenden Spalten zu projizieren. dplyr ist aber bezüglich der Verarbeitung von Data Frames sehr intuitiv und funktional, sodass wir früher oder später viele Operationen auf unserem Data Frame verketten werden. So erreichen wir die Mächtigkeit von SQL und mehr. Die funktionale Syntax aus dem letzten Beispiel wird dann ganz schnell unleserlich, da die Verabeitungsreihenfolge (zuerst filter(), dann select()) nur durch Lesen des Codes von innen nach außen und von rechts nach links ersichtlich wird.

Daher geht dplyr einen Schritt weiter, indem es den eleganten Verkettungsoperator %>% aus dem magrittr-Paket importiert und zur Verfügung stellt. Dadurch werden die verschachtelten Ausdrücke in Sequenzen von Operationen gewandelt und somit sehr viel lesbarer und wartbarer:

1

2

3

4

5

6

7

8

9

10

11

select(filter(cars,Manufacturer=="Audi"),Model,Passengers)

Model Passengers

1 90 5

2 100 6

> cars %>%

+ filter(Manufacturer=="Audi") %>%

+ select(Model,Passengers)

Model Passengers

1 90 5

2 100 6

Diese in meinen Augen geniale Syntax durch den neuen Operator %>% erlaubt einen sequenziellen Aufbau der Operationen auf einem Data Frame. Benutzer der Unix-Kommandozeile werden hier leicht die Analogie zu Pipes erkennen. Ganz abstrakt kann man sagen, dass damit folgende Operationen äquivalent sind:

Traditioneller Funktionsaufruf	Verkettung mit %>%
f(a,b)	a %>% f(b)
f(a,b,c)	a %>% f(b,c)
g(f(a,b),c)	a %>% f(b) %>% g(c)

Weiteres erklärt die Dokumentation zum %>%-Operator im Paket magrittr mithilfe
des Befehls ?magrittr::‘%>%‘.

Neue Variablen

Durch die Funtionen select() und filter() können wir aus Data Frames Spalten projizieren und Zeilen selektieren. Ergebnisse neuer Ausdrücke entstehen hingegen mit dem Verb mutate():

1

2

3

4

5

6

7

8

9

10

11

12

13

14

> # Mit Umrechnung der Mileage in Verbrauch und des

> # Kaufpreises von USD in EUR

> cars2 <-

+ cars %>%

+ filter(Manufacturer=="Audi") %>%

+ mutate(l_100km = 235 / MPG.city,

+ eur = Min.Price * 1000 / 1.1) %>%

+ select(Model,Passengers,l_100km,eur)

> cars2

Model Passengers l_100km eur

1 90 5 11.75000 23545.45

2 100 6 12.36842 28000.00

> class(cars2)

[1] "data.frame"

Im obigen Beispiel wird zunächst auf den Hersteller Audi selektiert und danach auf einen Streich zwei neue Spalten eingeführt, l_100km und eur. Durch Zuweisen auf eine neue Variable wird das fertige Ergebnis dauerhaft gespeichert. Hierbei handelt es sich wieder um ein natives Data Frame-Objekt. Die Operation transmute() arbeitet analog zu mutate(), verwirft aber nach Bildung der Ausdrücke alle nicht genannten Spalten. Somit können wir obiges Beispiel auch wie folgt schreiben:

1

2

3

4

5

6

7

8

9

10

cars3 <-

+ cars %>%

+ filter(Manufacturer=="Audi") %>%

+ transmute(Model = Model, Passengers = Passengers,

+ l_100km = 235 / MPG.city,

+ eur = Min.Price * 1000 / 1.1)

cars3

Model Passengers l_100km eur

1 90 5 11.75000 23545.45

2 100 6 12.36842 28000.00

Aggregate

Neben der Selektion von Zeilen und Spalten sowie der Bildung abgeleiteter Ausdrücke ist bei Datenbanktabellen die Gruppierung und Aggregation mit GROUP BY eine sehr wichtige Operation. Dies gilt auch für Data Frames in R, wenngleich hier der Funktionsumfang über diverse Funktionen wie table() oder aggregate() verteilt ist und wenig intuitiv ist.

Hier bringt dplyr ebenfalls eine großartige Verbesserung mit. Das entsprechende Verb heißt group_by(). Diese Operation wird zusammen mit einer Spaltenliste auf ein Data Frame angewendet:

1

2

3

grp_cars <- cars %>% group_by(Manufacturer)

> class(grp_cars)

[1] "grouped_df" "tbl_df" "tbl" "data.frame"

Das Ergebnis von group_by() ist ein Objekt, das “mehr” ist als ein Data Frame, sondern auch noch einige spezifische Strukturinformationen von dplyr enthält. In unserem Beispiel sind dies Indizes von Zeilen, die zum gleichen Hersteller gehören. Das ursprüngliche Data Frame wird hierbei nicht kopiert, sondern nur eingebettet.

Nach Anwenden einer group_by()-Operation ist das Data Frame optimal vorbereitet für die eigentliche Aggregation mit summarise():

1

2

3

4

5

6

7

8

> sum_cars <- cars %>%

+ group_by(Manufacturer) %>%

+ summarise(nCars = n(), avg_price = mean(Min.Price))

> str(sum_cars)

Classes ‘tbl_df’, ‘tbl’ and ’data.frame’: 32 obs. of 3 variables:

$ Manufacturer: Factor w/ 32 levels "Acura","Audi",..: 1 2 3 4 5 6 7 8 9 10 ...

$ nCars : int 2 2 1 4 2 8 1 2 6 2 ...

$ avg_price : num 21.1 28.4 23.7 20.8 35.2 ...

Das Resultat von summarise() ist wieder ein Data Frame, das neben den ursprünglichen Gruppierungskriterien nur noch die Aggregate enthält.

Daten in Reih’ und Glied

Zwischen Relationalen Datenbanken und R-Data Frames besteht ein wesentlicher konzeptioneller Unterschied: Die Ergebnisse eines SELECT-Befehls haben keine definierte Reihenfolge, so lange die Zeilen nicht mit der Klausel ORDER BY festgelegt wird. Im Gegensatz dazu haben die Zeilen von Data Frames eine konstante Reihenfolge, die sich aus der Anordnung derWerte in den Spaltenvektoren ergibt.

Dennoch ist es manchmal wünschenswert, Data Frames umzusortieren, um eine fachliche Reihenfolge abzubilden. Hierzu dient in dplyr das Verb arrange(), das im Standard-R weitgehend der Indizierung eines Data Frames mit Ergebnissen der order()-Funktion entspricht, aber syntaktisch eleganter ist:

1

2

3

4

5

6

7

8

9

10

cars %>%

+ arrange(desc(Horsepower),Manufacturer) %>%

+ select(Manufacturer, Model, Horsepower,Min.Price) %>%

+ slice(1:5)

Manufacturer Model Horsepower Min.Price

1 Chevrolet Corvette 300 34.6

2 Dodge Stealth 300 18.5

3 Cadillac Seville 295 37.5

4 Infiniti Q45 278 45.4

5 Mazda RX-7 255 32.5

Dieses Beispiel hat zum Ziel, die fünf PS-stärksten Autos zu selektieren. Die arrange()-Funktion sortiert hier zunächst absteigend nach der PS-Stärke, dann aufsteigend nach Herstellername. Die Selektion der 5 ersten Zeilen erfolgt mit der hilfreichen Funktion slice(), die aus einem Data Frame Zeilen anhand ihrer Reihenfolge selektiert.

Fazit und Ausblick

Mit dplyr wird die Arbeit mit Data Frames stark verbessert: Im Vergleich zu “nacktem” R bringt das Paket eine klarere Syntax, abgerundete Funktionalität und bessere Performance. In der Kürze dieses Artikels konnte ich dies nur oberflächlich anreissen. Daher verweise ich auf die vielen Hilfe-Seiten, Vignetten und Internet-Videos zum Paket. Im zweiten Teil dieses Artikels werde ich auf einige fortgeschrittene Features von dplyr eingehen, z.B. die Verknüpfung von Data Frames mit Joins, die Window-Funktionen und die Verwendung von Datenbanken als Backend.

Weiter zu R Data Frames meistern mit dplyr – Teil 2.

Interview – Mit Data Science Kundenverhalten vorhersagen

November 10, 2016/2 Comments/in Big Data, Business Analytics, Carrier, Data Mining, Data Science, Gerneral, Interview mit CIO, Interviews, Predictive Analytics, Statistics /by Benjamin Aunkofer

Frau Dr. Eva-Marie Müller-Stüler ist Associate Director in Decision Science der KPMG LLP in London. Sie absolvierte zur Diplom-Mathematikerin an der Technischen Universität München, mit einem einjährigen Auslandssemester in Tokyo, und promovierte an der Philipp Universität in Marburg.

Read this article in English:
“Interview – Using Decision Science to forecast customer behaviour”

Data Science Blog: Frau Dr. Müller-Stüler, welcher Weg hat Sie bis an die Analytics-Spitze der KPMG geführt?

Ich hatte schon immer viel Spaß an analytischen Fragestellungen, aber auch ein großes Interesse an Menschen und Finance. Die Frage wie Menschen ticken und Entscheidungen treffen finde ich unglaublich spannend. Im Mathematikstudium und auch bei der Doktorarbeit kamen dann das Auswerten von großen Datenmengen und das Programmieren von Algorithmen hinzu. Die solide mathematische Ausbildung kombiniert mit dem spezifischen Branchen- und Finanzverständnis ermöglicht es mir das Geschäftsmodell meiner Kunden zu verstehen und Methoden zu entwickeln, die den Markt verändern und neue Wege finden.

Data Science Blog: Welche Analysen führen Sie für Ihre Kundenaufträge durch? Welche Vorteile generieren Sie für Ihre Kunden?

Unser Team beschäftigt sich hauptsächlich mit Behaviour und Customer Science. Daher auch der Slogan „We understand human behaviour and we change it“. Unser Focus ist der Mensch (z.B. Kunde oder der Mitarbeiter) und die Frage, wie wir ihn durch das Verständnis seiner Datenartefakte im Verhalten ändern bzw. zukünftiges Verhalten vorhersagen können. Auf dieser Basis entwickeln wir Always-on forecasting Modelle, die es dem Mandanten ermöglichen, bereits im Vorfeld zu agieren. Das kann z.B. bedeuten, durch ortgenaue Informationen spezifische Kundennachfrage an einem bestimmten Standort vorherzusagen, wie sie verbessert oder in die gewünschte Richtung beeinflusst werden kann oder durch welche Maßnahmen bzw. Promotions welcher Kundentyp optimal erreicht wird. Oder auch die Frage wo und mit welcher Produktmischung am besten ein neues Geschäft eröffnet werden soll, ist mit Predictive Analytics viel genauer vorherzusagen als durch herkömmliche Methoden.

Data Science Blog: Welche Voraussetzungen müssen erfüllt sein, damit prädiktive Analysen für Kundenverhalten adäquat funktionieren?

Die Daten müssen natürlich eine gewisse Qualität und Historie haben um z. B. auch Trends und Zyklen zu erkennen. Oft kann man sich aber auch über die Einbindung neuer Datenquellen einen Vorteil erschaffen. Dabei ist Erfahrung und Kreativität enorm wichtig, um zu verstehen was möglich ist und die Qualität verbessert oder ob etwas nur für mehr Rauschen sorgt.

Data Science Blog: Welche externen Datenquellen müssen Sie dafür einbinden? Wie behandeln Sie unstrukturierte Daten?

Hier in England ist man – was externe Datenquellen angeht – schon sehr verwöhnt. Wir benutzen im Schnitt an die 10.000 verschiedene Signale, die je nach Fragestellung unterschiedlich seien können: z. B. die Zusammensetzung der Bevölkerung, Nahverkehrsinformationen, die Nähe von Sehenswürdigkeiten, Krankenhäusern, Schulen, Kriminalitätsraten und vieles mehr. Der Einfluss eines Signals ist bei jedem Problem unterschiedlich. So kann eine hohe Anzahl an Taschendiebstählen ein Zeichen dafür sein, dass in der Gegend viel los ist und die Menschen im Schnitt viel Bargeld bei sich tragen. Das kann z. B. für einen Fast Food-Retailer in der Innenstadt durchaus einen positiven Einfluss auf sein Geschäft haben in einer anderen Gegend aber das Gegenteil bedeuten.

Data Science Blog: Welche Möglichkeiten bietet Data Science für die Forensik bzw. zur Betrugserkennung?

Da jeden Kunden tausende Datensignale umgeben und er durch sein Verhalten weitere produziert und aussendet, kann man gerade beim Online-Geschäft schon ein ziemlich gutes Bild über die Person bekommen. Jede Art von Mensch hat ein gewisses Verhaltensmuster und das gilt auch für Betrüger. Diese Muster muss man nur rechtzeitig erkennen oder vorherzusagen lernen.

Data Science Blog: Welche Tools verwenden Sie bei Ihrer Arbeit? In welchen Fällen setzten Sie auf proprietäre Software, wann hingegen auf Open Source?

Das hängt vom Arbeitsschritt und dem definierten Ziel ab. Wir unterscheiden unser Team in unterschiedliche Gruppen: Unsere Data Wrangler (die für das Extrahieren, Erzeugen und Aufbereiten der Daten zuständig sind) arbeiten mit anderen Tools als z. B. unsere Data Modeller. Im Grunde umfasst es die gesamte Palette von SQL Server, R, Python, manchmal aber auch Matlab oder SAS. Immer häufiger arbeiten wir auch mit auf Cloud-Technologie basierenden Lösungen. Data Visualisation und Dashboards in Qlik, Tableau oder Alteryx geben wir in der Regel jedoch an andere Teams weiter.

Data Science Blog: Wie sieht Ihrer Erfahrung nach der Arbeitsalltag als Data Scientist nach dem morgendlichen Café bis zum Feierabend aus?

Meine Rolle ist vielleicht am besten zu beschreiben als der Player-Coach. Da läuft von allem etwas mit ein. Am Anfang eines Projektes geht es vor Allem darum, mit den Mandaten die Fragestellung zu erarbeiten und das Projekt zu gewinnen. Teil dessen ist auch neue Ideen und Methoden zu entwickeln. Während eines Projektes sind das Team Management, der Wissenstransfer im Team, der Review und das Hinterfragen der Modelle meine Hauptaufgaben. Am Schluss kommt dann der endgültige Sign-off des Projektes. Da ich oft mehrere Projekte in unterschiedlichen Stadien gleichzeitig leite, wird es garantiert nie langweilig.

Data Science Blog: Sind gute Data Scientists Ihrer Erfahrung nach tendenziell eher Beratertypen oder introvertierte Nerds?

Das hängt so ein bisschen davon ab wo man seinen Schwerpunkt sieht. Als Data Visualizer oder Data Artist geht es darum die Informationen auf das wesentlich zu reduzieren und toll und verständlich darzustellen. Dafür braucht man Kreativität und ein gutes Verständnis für das Geschäft und einen sicheren Umgang mit den Tools.

Der Data Analyst beschäftigt sich vor Allem mit dem „Slice and Dice“ von Data. Ziel ist es, die Vergangenheit zu analysieren und Zusammenhänge zu erkennen. Es ist wichtig zusätzlich zu dem finanziellen Wissen auch gute mathematische Fähigkeiten zu haben.

Der Data Scientist ist der mathematischste von allen. Er beschäftigt sich damit aus den Daten tiefere Zusammenhänge zu erkennen und Vorhersagen zu treffen. Dabei geht es um die Entwicklung von komplizierten Modellen oder auch Machine Learning Algorithmen. Ohne eine gute mathematische Ausbildung und Programmierkenntnisse ist es leider nicht möglich die Sachen in voller Tiefe zu verstehen. Die Gefahr falsche Schlüsse zu ziehen oder Korrelationen zu interpretieren, die sich aber nicht bedingen ist sehr groß. Ein einfaches Beispiel hierfür ist, dass im Sommer, wenn das Wetter schön ist, mehr Menschen Eis essen und in Seen baden gehen. Daher lässt sich eine eindeutige Korrelation zwischen Eis essen und der Anzahl an Ertrunkenen zeigen, obwohl nicht das Eis essen zum Ertrinken führt sondern die beeinflussende Variable die Temperatur ist. Daher ist ein Doktor in einem mathematiknahen Fach schon wichtig.

Genauso ist aber für den Data Scientist auch das entsprechende Finanz- und Branchenwissen wichtig, denn seine Erkenntnisse und Lösung müssen relevant für den Kunden sein und deren Probleme lösen oder Prozesse verbessern. Die tollste AI Maschine bringt keiner Bank einen Wettbewerbsvorteil, wenn sie den Eisverkauf auf Basis des Wetters vorhersagt. Das kann zwar rechnerisch 100% richtig sein, hat aber keine Relevanz für den Kunden.

Es ist im Grunde wie in anderen Bereichen (z. B. der Medizin) auch. Es gibt viele verschiedene Schwerpunkte und für ernsthafte Probleme wendet man sich am besten an einen Spezialisten, damit man keine falschen Schlüsse zieht.

Data Science Blog: Für alle Studenten, die demnächst ihren Bachelor, beispielsweise in Informatik, Mathematik oder Wirtschaftslehre, abgeschlossen haben, was würden sie diesen jungen Damen und Herren raten, wie sie gute Data Scientists werden können?

Nie aufhören mit dem Lernen! Der Markt entwickelt sich derzeit unglaublich schnell und hat so viele tolle Seiten. Man sollte einfach mit Leidenschaft, Begeisterung und Kreativität dabei sein und Spaß an der Erkennung von Mustern und Zusammenhängen haben. Wenn man sich dann noch mit interessanten und inspirierenden Menschen umgibt, von denen man noch mehr lernen kann, bin ich zuversichtlich, dass man eine tolle Arbeitszeit haben wird.

ABC-XYZ-Analyse

October 20, 2016/0 Comments/in Business Analytics, Business Intelligence, Data Mining, Data Science, Data Science Hack, Python, Statistics, Tutorial /by Benjamin Aunkofer

Die ABC-XYZ-Analyse ist eine aussagekräftige Analyse für die Strategiefindung in der Warenwirtschaft und Logistik bzw. im Supply Chain Management. Die Analyse basiert auf der Vorstellung einer Pareto-Verteilung, die darauf hindeutet, dass oftmals eine kleine Menge eines großen Ganzen einen unverhältnismäßig großen Einfluss auf eben dieses große Ganze hat.

Die ABC-XYZ-Analyse beinhaltet im ersten Schritt eine ABC- und im zweiten Schritt eine XYZ-Analyse. Im dritten Schritt werden die Ergebnisse in einer Matrix zusammengeführt. In diesem Artikel erläutere ich nicht, wofür eine ABC-XYZ-Analyse dient und wie die Ergebnisse zu interpretieren sind, hier kann ich jedoch auf einen älteren Artikel “ABC-XYZ-Analyse” – www.der-wirtschaftsingenieur.de vom 3. Mai 2011 von mir verweisen, der vorher lesenswert ist, wenn kein Vorwissen zur ABC-XYZ-Analyse vorhanden ist.

Die Vorarbeit

Für die ABC- und XYZ-Analyse benötigen wir folgende Python-Bibliotheken:

1

2

3

4

import pandas as pd

import numpy as np

import random as random

import matplotlib.pyplot as pyplot

Wir laden die EKPO-Tabelle in ein DataFrame (Datenstruktur der Pandas-Bibliothek):

1 2	EKPO = pd.read_csv("[PFAD]\EKPO.csv", delimiter=';', thousands='.', decimal=',')

Die Datei stammt aus einem SAP-Testsystem und steht hier zum Download bereit:

SAP.EKPO

Wir benötigen daraus nur folgende Zeilen:

1 2	EKPO_X = EKPO[['MATNR', 'MATKL', 'MENGE', 'PEINH', 'NETPR', 'NETWR']].copy()

Jetzt kommt der erste Kniff: Das Feld “MENGE” im SAP beschreibt die Menge in der jeweiligen Mengeneinheit (z. B. Stück, Meter oder Liter). Da wir hier jedoch nicht den genauen Verbrauch vorliegen haben, sondern nur die Einkaufsmenge (indirekt gemessener Verbrauch), sollten wir die Menge pro Preiseinheit “PEINH” berücksichtigen, denn nach dieser Preiseinheitsmenge erfolgt der Einkauf.

1 2	EKPO_X['Preiseinheitsmenge'] = EKPO_X['MENGE'] / EKPO_X['PEINH']

Für die Preiseinheitsmenge ein Beispiel:
Sie kaufen sicherlich pro Einkauf keine 3 Rollen Toilettenpapier, sondern eine oder mehrere Packungen Toilettenpapier. Wenn Sie zwei Packung Toilettenpapier für jeweils 2 Euro kaufen, die jeweils 10 Rollen beinhalten, ist die Preiseinheit = 10 und die Preiseinheitsmenge => 20 gekaufte Toilettenrollen / 10 Rollen pro Packung = 2 Packungen Toilettenpapier.

Nun haben wir also unsere für den Einkauf relevante Mengeneinheit. Jetzt sortieren wir diese Materialeinkäufe primär nach dem Umsatzvolumen “NETWR” absteigend (und sekundär nach der Preiseinheitsmenge aufsteigend, allerdings spielt das keine große Rolle):

1	EKPO_X = EKPO_X.sort_values(by = ['NETWR', 'Preiseinheitsmenge'], ascending=[False, True]) # Sortierung nach Umsatzvolumen pro Bestellung absteigend

Einige Störfaktoren müssen noch bereinigt werden. Erstens sollen Einträge mit Preisen oder Umsätzen in Höhe von 0,00 Euro nicht mehr auftauchen:

1 2	EKPO_X = EKPO_X[(EKPO_X.NETPR != 0) & (EKPO_X.NETWR != 0)]

Zweitens gibt es Einkäufe, die ein Material ohne Materialnummer und/oder ohne Materialklasse haben. Bei einer Zusammenfassung (Aggregation) über die Materialnummer oder die Materialklasse würden sich diese “leeren” Einträge als NULL-Eintrag bündeln. Das wollen wir vermeiden, indem wir alle NULL-Einträge mit jeweils unterschiedlichen Zufallszahlen auffüllen.

1

2

EKPO_X.MATNR[EKPO_X.MATNR.isnull() == True] = EKPO_X.MATNR[EKPO_X.MATNR.isnull() == True].apply(lambda x: random.random()) # Manche MATNR fehlen (NULL), diese füllen wir mit zufälligen Werten auf. Dabei ist es natürlich wichtig, dass die Zufallszahl für jede Zeile neu generiert wird! EKPO_X.MATNR.fillna(random.random()) funktioniert nicht, denn hier würde ein gleicher Wert alle NaN-Werte ersetzen

ABC – Analyse:

Nun geht es an die eigentliche ABC-Analyse, dafür müssen wir die Gruppierung der Materialien vornehmen. Gleich vorweg: Dies sollte man eigentlich über die einzelnen Materialnummern machen, da dies jedoch in der Visualisierung (auf Grund der hohen Anzahl und Vielfältigkeit) etwas aufwändiger ist, machen wir es über die Materialklassen. Wir gehen dabei einfach davon aus, dass die Materialklassen relativ homogene Materialien zusammenfassen und somit auch das Verbrauchs-/Einkaufverhalten innerhalb einer Gruppe nicht sonderlich viel Abweichung aufweist.

Materialklasse

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

# Aggregation über die Materialklasse, Aufsummierung der Umsätze, Mengen und Volumen

MATKL_MENGEN = (EKPO_X.MENGE.groupby(EKPO_X.MATKL).sum()).to_frame()

MATKL_PREISEINHEIT_MENGE = (EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATKL).sum()).to_frame()

MATKL_VOLUMEN = (EKPO_X.NETWR.groupby(EKPO_X.MATKL).sum()).to_frame()

# Aggregation über die Materialklasse, Berechnung des Durchschnittpreises (ist bei einer Materialklasse, allerdings wenig sinnvoll!)

MATKL_Preise = (EKPO_X.NETPR.groupby(EKPO_X.MATKL).mean()).to_frame()EKPO_G = MATKL_MENGEN.join(MATKL_PREISEINHEIT_MENGE, how='left')

# Zusammenfügen der Ergebnisse (Left-Join)

EKPO_G = EKPO_G.join(MATKL_Preise, how='left')

EKPO_G = EKPO_G.join(MATKL_VOLUMEN, how='left')

EKPO_G = EKPO_G.sort_values(['NETWR'], ascending=False)

# Berechnung der kumulierten Umsätze und Mengen (Beachte: Vorher muss nach Umsätzen absteigend sortiert worden sein! (siehe oben)

EKPO_G['Volumen_kumuliert'] = EKPO_G.NETWR.cumsum()

EKPO_G['Menge_kumuliert'] = EKPO_G.MENGE.cumsum()

Materialnummer

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

MATNR_MENGEN = EKPO_X.MENGE.groupby(EKPO_X.MATNR).sum()

MATNR_PREISEINHEIT_MENGE = EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATNR).sum()

MATNR_VOLUMEN = EKPO_X.NETWR.groupby(EKPO_X.MATNR).sum()

MATNR_Preise = EKPO_X.NETPR.groupby(EKPO_X.MATNR).mean()MATNR_MENGEN = MATNR_MENGEN.to_frame()

MATNR_PREISEINHEIT_MENGE = MATNR_PREISEINHEIT_MENGE.to_frame()

MATNR_Preise = MATNR_Preise.to_frame()

MATNR_VOLUMEN = MATNR_VOLUMEN.to_frame()EKPO_G = MATNR_MENGEN.join(MATNR_PREISEINHEIT_MENGE, how='left')

EKPO_G = EKPO_G.join(MATNR_Preise, how='left')

EKPO_G = EKPO_G.join(MATNR_VOLUMEN, how='left')

EKPO_G = EKPO_G.sort_values(['NETWR'], ascending=False)

EKPO_G['Volumen_kumuliert'] = EKPO_G.NETWR.cumsum()

EKPO_G['Menge_kumuliert'] = EKPO_G.MENGE.cumsum()

Nun können wir uns ganz im Sinne der ABC-Analyse die typische Pareto-Verteilung der kumulierten Umsätze (Umsatzgrößen absteigend sortiert) ansehen:

1 2	EKPO_G[['Menge_kumuliert','Volumen_kumuliert']].plot([EKPO_G.Menge_kumuliert, EKPO_G.Volumen_kumuliert], color=['red','pink'], figsize=[20,10], fontsize=8, title='Kumulierte Werte - Sortierung nach Materialklassen-Volumen')

abc_analyse_sap_netwr_menge_kumulierte_kurve_pareto

Die X-Achse zeigt die Materialklassen von links nach rechts in der Sortierung nach dem Umsatzvolumen (größester Umsatz links, kleinster Umsatz rechts). Die Y-Achse zeigt den Betrag der Umsatzhöhe (Euro) bzw. der Menge (Preiseinheitsmenge). Die Kurve der Menge ist mit Vorsicht zu bewerten, da primär nach dem Umsatz und nicht nach der Menge sortiert wurde.

Klassifikation:

Nun kommen wir zur Klassifikation. Hier machen wir es uns sehr einfach: Wir gehen einfach davon aus, dass 80% des Wertbeitrages aller Umsätze von etwa 20% der Materialien (hier: Materialklassen) umfassen und klassifizieren daher über feste relative Größen:

1

2

3

4

EKPO_G['ABC_Gruppe'] = "C" # Erstmal sind alle Materialien der C-Gruppe zugeordnet

EKPO_G['ABC_Gruppe'][EKPO_G.Volumen_kumuliert <= EKPO_G.NETWR.sum() / 100 * 95] = 'B' # Materialien, deren kumuliertes Volumen maximal 95% des Gesamtvolumens umfassen, sind Gruppe B

EKPO_G['ABC_Gruppe'][EKPO_G.Volumen_kumuliert <= EKPO_G.NETWR.sum() / 100 * 80] = 'A' # Materialien, deren kumuliertes Volumen maximal 80% des Gesamtvolumens umfassen, sind Gruppe A

Hinweis:
Intelligenter wird so eine Klassifikation, wenn wir den steilsten Anstieg innerhalb der kumulierten Volumen (die zuvor gezeigte Kurve) ermitteln und danach die Grenzen für die A-, B-, C-Klassen festlegen.

Optional: Farben für die Klassen festlegen (für die nachfolgende Visualisierung)

1

2

3

4

EKPO_G['Color'] = 'red'

EKPO_G['Color'][EKPO_G['ABC_Gruppe'] == 'B'] = 'orange'

EKPO_G['Color'][EKPO_G['ABC_Gruppe'] == 'C'] = 'green'

Jetzt Aggregieren wir über die ABC-Gruppe:

1

2

3

4

5

6

7

GruppenWerte = EKPO_G.groupby(['ABC_Gruppe'])

GruppenVolumen = (GruppenWerte.NETWR.sum()).to_frame()

GruppenMengen = (GruppenWerte.Preiseinheitsmenge.sum()).to_frame()

# Wieder zusammenfügen

GruppenVolumenMengen = GruppenVolumen.join(GruppenMengen)

Das Ergebnis:

1

2

3

4

5

6

7

8

9

GruppenVolumenMengen

Out:

NETWR Preiseinheitsmenge

ABC_Gruppe

A 6190725.01 175748.29

B 1231070.86 199599.24

C 408128.45 99745.63

Schauen wir uns nun die Verteilung der Werte und Mengen zwischen den Klassen A, B und C an:

1 2	GruppenVolumenMengen.plot(kind='bar', width=0.90, xlim=[0,1000], figsize=[10,5], yticks=GruppenVolumenMengen.NETWR)

Es ist recht gut erkennbar, dass die Gruppe A deutlich mehr Umsatzvolumen (also Wertbeitrag) als die Gruppen B und C hat. Allerdings hat sie auch eine höhere Bestellmenge, wie jedoch nicht proportional von C über B zu A ansteigt wie das Umsatzvolumen.

Nachfolgend sehen wir die Klassifikation nochmal nicht kumuliert über die Umsatzvolumen der Materialien (Materialklassen):

1 2	EKPO_G[['NETWR']].plot(kind='bar', figsize=[20,10], legend = True, color=EKPO_G.Color, alpha=0.65, title='ABC - Analyse')

XYZ – Analyse

Für die XYZ-Analyse berechnen wir den arithmetischen Mittelwert, die Standardabweichung und die Summe aller Mengen pro Materialklasse [‘MATKL’] (oder alternativ, der einzelnen Materialnummern [‘MATNR’]) über eine Aggregation:

1

2

3

4

5

6

Material_Menge = EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATKL).agg({'mean', 'std', 'sum'})

#Oder mit dem Material: Material_Menge = EKPO_X.Preiseinheitsmenge.groupby(EKPO_X.MATNR) .agg({'mean', 'std', 'sum'})

#Leider ergeben sich einige NaNs bei der Standardabweichung, da ein Material oder eine Materialklasse nur eine einzige Buchung haben kann, diese müssen wir bereinigen (hier: mit Nullen auffüllen):

Material_Menge = Material_Menge.fillna(0)

Die XYZ-Analyse soll aufzeigen, welche Materialien (hier: Materialklassen) in stabilen Mengen verbraucht (hier: eingekauft) werden und welche größere Schwankungen hinsichtlich der Verbrauchsmenge (hier: Einkaufsmenge) aufweisen. Dazu berechnen wir den Variationskoeffizienten:

$Variationskoeffizient = \frac{Standardabweichung}{Mittelwert}$

Wir berechnen diesen Variationskoeffizienten und sortieren das DataFrame nach diesem aufsteigend:

1

2

3

Material_Menge['Variationskoeffizient'] = Material_Menge['std'] / Material_Menge['mean']

Material_Menge = Material_Menge.sort_values(['Variationskoeffizient'], ascending = True)

Klassifikation:

Nun klassifizieren wir die Materialien (Materialklassen) über den Variationskoeffizienten in XYZ-Klassen. Dabei gehen wir davon aus, dass Materialien/Materialklassen, die einen Variationskoeffizienten von bis zu 70% des Maximalwertes aufweisen, in die Y-Klasse fallen. Solche, die nur maximal 20% des Maximalwertes aufweisen, fallen in die X-Klasse:

1

2

3

4

Material_Menge['XYZ_Gruppe'] = 'Z'

Material_Menge['XYZ_Gruppe'][Material_Menge.Variationskoeffizient <= Material_Menge.Variationskoeffizient.max() / 100 * 70] = 'Y'

Material_Menge['XYZ_Gruppe'][Material_Menge.Variationskoeffizient <= Material_Menge.Variationskoeffizient.max() / 100 * 20] = 'X'

Auch hier gilt analog zur ABC-Analyse: Intelligente Klassifikation erfolgt über die Analyse der Kurve der kumulierten Variationskoeffizienten. Die Grenzen der Klassen sollten idealerweise zwischen den steilsten Anstiegen (bzw. die größten Wertedifferenzen) zwischen den Werten der kumulierten Variationskoeffizienten-Liste gezogen werden.

Optional: Farben fürs Plotten setzen.

1

2

3

4

Material_Menge['Color'] = 'red'

Material_Menge['Color'][Material_Menge.XYZ_Gruppe == 'Y'] = 'orange'

Material_Menge['Color'][Material_Menge.XYZ_Gruppe == 'X'] = 'green'

Jetzt schauen wir uns mal die Verteilung der Materialien hinsichtlich des Variationskoeffizienten an:

1 2	Material_Menge.Variationskoeffizient.plot(kind='bar', width=0.90, xlim=[0,1000], figsize=[20,5], rot=90, color=Material_Menge.Color, title='XYZ - Analyse')

Die meisten Materialklassen haben einen recht niedrigen Variationskoeffizienten, sind im Einkauf (und daher vermutlich auch im Verbrauch) recht stabil. Die Materialklasse 0004 hingegen ist einigen Mengenschwankungen unterworfen. In der ABC-Analyse ist diese Materialklasse 0004 als B-Gruppe klassifiziert.

ABC-XYZ-Analyse

Nun möchten wir also die zuvor erstellte ABC-Klassifikation mit der XYZ-Klassifikation zusammen bringen.

Dafür fügen wir die beiden Pandas.DataFrame über den Index (hier die Materialklasse ‘MATKL’, im anderen Fall das Material ‘MATNR’) zusammen:

1 2	XYZ_ABC = pd.merge(EKPO_G, Material_Menge, left_index = True, right_index = True, how='left')

Die Zusammenfassung als Kreuztabelle:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

pd.crosstab(XYZ_ABC.ABC_Gruppe, XYZ_ABC.XYZ_Gruppe, margins=True)

Out:

X Y Z All

A 17 1 0 18

B 19 1 1 21

C 69 2 0 71

All 105 4 1 110

Für die Interpretation dieser Ergebnisse verweise ich erneut auf den Artikel bei der-wirtschaftsingenieur.de.

Warenkorbanalyse in R

October 8, 2016/1 Comment/in Business Analytics, Data Mining, Data Science, Data Science Hack, Mathematics, R Statistics, Statistics /by Daniela Keller

Was ist die Warenkorbanalyse?

Die Warenkorbanalyse ist eine Sammlung von Methoden, die die beim Einkauf gemeinsam gekauften Produkte oder Produktkategorien aus einem Handelssortiment untersucht. Ziel der explorativen Warenkorbanalyse ist es, Strukturen in den Daten zu finden, so genannte Regeln, die beschreiben, welche Produkte oder Produktkategorien gemeinsam oder eben nicht gemeinsam gekauft werden.

Beispiel: Wenn ein Kunde Windeln und Bier kauft, kauft er auch Chips.

Werden solche Regeln gefunden, kann das Ergebnis beispielsweise für Verbundplatzierungen im Verkaufsraum oder in der Werbung verwendet werden.

Datenaufbau

Die Daten, die für diese Analyse untersucht werden, sind Transaktionsdaten des Einzelhandels. Meist sind diese sehr umfangreich und formal folgendermaßen aufgebaut:

Ausschnitt eines Beispieldatensatzes: Jede Transaktion (= Warenkorb = Einkauf) hat mehrere Zeilen, die mit der selben Transaktionsnummer (Spalte Transaction) gekennzeichnet sind. In den einzelnen Zeilen der Transaktion stehen dann alle Produkte, die sich in dem Warenkorb befanden. In dem Beispiel sind zudem noch zwei Ebenen von Produktkategorien als zusätzliche Informationen enthalten.

Es gibt mindestens 2 Spalten: Spalte 1 enthält die Transaktionsnummer (oder die Nummer des Kassenbons, im Beispielbild Spalte Transaction), Spalte 2 enthält den Produktnamen. Zusätzlich kann es weitere Spalten mit Infos wie Produktkategorie, eventuell in verschiedenen Ebenen, Preis usw. geben. Sind Kundeninformationen vorhanden, z.B. über Kundenkarten, so können auch diese Informationen enthalten sein und mit ausgewertet werden.

Beschreibende Datenanalyse

Die Daten werden zunächst deskriptiv, also beschreibend, analysiert. Dazu werden z.B. die Anzahl der Transaktionen und die Anzahl der Produkte im Datensatz berechnet. Zudem wird die Länge der Transaktionen, also die Anzahl der Produkte in den einzelnen Transaktionen untersucht. Dies wird mit deskriptiven Maßzahlen wie Minimum, Maximum, Median und Mittelwert in Zahlen berichtet sowie als Histogramm grafisch dargestellt, siehe folgende Abbildung.

Histogramm der Längenverteilung der Transaktionen.

Die häufigsten Produkte werden ermittelt und können gesondert betrachtet werden. Als Visualisierung kann hier ein Balkendiagramm mit den relativen Häufigkeiten der häufigsten Produkte verwendet werden, wie im folgenden Beispiel.

Relative Häufigkeiten der häufigsten Produkte, hier nach relativer Häufigkeit größer 0,1 gefiltert.

Ähnliche Analysen können bei Bedarf auch auf Kategorien-Ebene oder nach weiteren erhobenen Merkmalen selektiert durchgeführt werden, je nachdem, welche Informationen in den Daten stecken und welche Fragestellungen für den Anwender interessant sind.

Verbundanalyse

Im nächsten Schritt wird mit statistischen Methoden nach Strukturen in den Daten gesucht, auch Verbundanalyse genannt. Als Grundlage werden Ähnlichkeitsmatrizen erstellt, die für jedes Produktpaar die Häufigkeit des gemeinsamen Vorkommens in Transaktionen bestimmen. Solch eine Ähnlichkeitsmatrix ist zum Beispiel eine Kreuztabelle in der es für jedes Produkt eine Spalte und eine Zeile gobt. In den Zellen in der Tabelle steht jeweils die Häufigkeit, wie oft dieses Produktpaar gemeinsam in Transaktionen in den Daten vorkommt, siehe auch folgendes Beispiel.

Ähnlichkeitsmatrix oder Kreuztabelle der Produkte: Frankfurter und Zitrusfrüchte werden in 64 Transaktionen zusammen gekauft, Frankfurter und Berries in 22 usw.

Auf Basis solch einer Ähnlichkeitsmatrix wird dann z.B. mit Mehrdimensionaler Skalierung oder hierarchischen Clusteranalysen nach Strukturen in den Daten gesucht und Gemeinsamkeiten und Gruppierungen gefunden. Die hierarchische Clusteranalyse liefert dann ein Dendrogram, siehe folgende Abbildung, in der ähnliche Produkte miteinander gruppiert werden.

Dendrogram als Visualisierung des Ergebnisses der hierarchischen Clusterananlyse. Ähnliche Produkte (also Produkte, die zusammen gekauft werden) werden zusammen in Gruppen geclustert. Je länger die vertikale Verbindungslinie ist, die zwei Gruppen oder Produkte zusammen fasst, um so unterschiedlicher sind diese Produkte bzw. Gruppen.

Assoziationsregeln

Schließlich sollen neben den Verbundanalysen am Ende in den Daten Assoziationsregeln gefunden werden. Es werden also Regeln gesucht und an den Daten geprüft, die das Kaufverhalten der Kunden beschreiben. Solch eine Regel ist zum Beispiel „Wenn ein Kunde Windeln und Bier kauft, kauft er auch Chips.“ Formal: {Windeln, Bier} → {Chips}

Für diese Regeln lassen sich statistische Maßzahlen berechnen, die die Güte und Bedeutung der Regeln beschreiben. Die wichtigsten Maßzahlen sind Support, Confidence und Lift:

Support ist das Signifikanzmaß der Regel. Es gibt an, wie oft die gefundene Regel in den Daten anzuwenden ist. Wie oft also die in der Regel enthaltenen Produkte gemeinsam in einer Transaktion vorkommen. In dem Beispiel oben: Wie oft kommen Windeln, Bier und Chips in einer Transaktion gemeinsam vor?

Confidence ist das Qualitätsmaß der Regel. Es beschreibt, wie oft die Regel richtig ist. In dem oben genanten Beispiel: Wie oft ist in einer Transaktion Chips enthalten, wenn auch Windeln und Bier enthalten sind?

Lift ist das Maß der Bedeutung der Regel. Es sagt aus wie oft die Confidence den Erwartungswert übersteigt. Wie ist die Häufigkeit des gemeinsamen Vorkommens von Windeln, Bier und Chips im Verhältlnis zur erwarteten Häufigkeit des Vorkommens, wenn die Ereignisse stochastisch unabhängig sind?

Algorithmen

In den Daten werden zunächst alle möglichen Regeln gesammelt, die einen Mindestwert an Support und Confidence haben. Die Mindestwerte werden dabei vom Nutzer vorgegeben. Da es sich bei Transaktionsdaten um große Datenmengen handelt und häufig große Anzahlen von Produkten enthalten sind, wird die Suche nach Regeln zu einem komplexen Problem. Es wurden verschiedene effiziente Algorithmen als Suchstrategien entwickelt, z.B. der APRIORI-Algorithmus von Agrawal und Srikant (1994), der auch im weiter unten vorgestellten Paket arules von R verwendet wird.

Sind die Assoziationsregeln gefunden, können Sie vom Nutzer genauer untersucht werden und z.B. nach den oben genannten Kennzahlen sortiert betrachtet werden, oder es werden die Regeln für spezielle Warenkategorien genauer betrachtet, siehe folgendes Beispiel.

Beispielausgabe von Regeln, hier die drei Regeln mit dem besten Lift. In der ersten Regel sieht man: Wenn Bier und Wein gekauft wird, wird auch Likör gekauft. Diese Regel hat einen Support von 0,002. Diese drei Produkte kommen also in 0,2 % der Transaktionen vor. Die Confidence von 0,396 zeigt, dass in 39,6 % der Transaktionen auch Likör gekauft wird, wenn Bier und Wein gekauft wird.

Umsetzung mit R

Die hier vorgestellten Methoden zur Warenkorbanalyse lassen sich mit dem Paket arules der Software R gut umsetzen. Im Folgenden gebe ich eine Liste von nützlichen Befehlen für diese Analysen mit dieser Software. Dabei wird mit data hier durchgehend der Datensatz der Transaktionsdaten bezeichnet.

1	summary(data)

Zusammenfassung des Datensatzes:

Anzahl der Transaktionen und Anzahl der Warengruppen
die häufigsten Produkte werden genannt mit Angabe der Häufigkeiten
Längenverteilung der Transaktionen (Anzahl der Produkte pro Transaktion): Häufigkeiten, deskriptive Maße wie Quartile
Beispiel für die Datenstruktur (Levels)

1	size(data)

Längen der Transaktionen (Anzahl der Produkte pro Transaktion)

1	hist(size(data))

Histogramm als grafische Darstellung der Transaktionslängen

1	itemFrequencyPlot(data, support=0.1)

rel. Häufigkeiten der einzelnen Produkte, hier nur die mit mindestens 10 % Vorkommen

1	crossTable(data)

Äquivalenzmatrix: Häufigkeiten der gemeinsamen Käufe für Produktpaare

1	dissJacc <- dissimilarity(data[, itemFrequency(data) > 0.05], method = "Jaccard", which = "items")

Unähnlichkeitsmatrix für die hierarchische Clusteranalyse

1	hcWard <- hclust(dissJacc, method = "ward.D")

Hierarchische Clusteranalyse

1	plot(hcWard)

Dendrogram der hierarchischen Clusteranalyse

1 2	rules <- apriori(data, parameter = list(support = 0.001, confidence = 0.2), control = list(verbose = FALSE))

Assoziationsregeln finden mit APRIORI-Algorithmus, hier Regeln mit mindestens 1% Support und 20 % Confidence

1	summary(rules)

Zusammenfassung der oben gefundenen Regeln (Anzahl, Eigenschaften Support, Confidence, Lift)

1	inspect(SORT(rules,by=“lift“)[1:5])

Einzelne Regeln betrachten, hier die laut Lift besten 5 Regeln

Referenzen:

Michael Hahsler, Kurt Hornik, Thomas Reutterer: Warenkorbanalyse mit Hilfe der Statistik-Software R, Innovationen in Marketing, S.144-163, 2006.
Michael Hahsler, Bettina Grün, Kurt Hornik, Christian Buchta, Introduciton to arules – A computational environment for mining association rules and frequent item sets. (Link zum PDF)
Rakesh Agrawal, Ramakrishnan Srikant, Fast algorithms for mining association rules, Proceedings of the 20th VLDB Conference Santiago, Chile, 1994
Software R: R Core Team (2016). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Link: R-Project.org.
Paket: arules: Mining Association Rules using R.

Beispieldatensatz: Groceries aus dem Paket arules

Benford-Analyse

September 21, 2016/1 Comment/in Audit Analytics, Mathematics, Python, Statistics, Tutorial /by Benjamin Aunkofer

Das Benfordsche Gesetz beschreibt eine Verteilung der Ziffernstrukturen von Zahlen in empirischen Datensätzen. Dieses Gesetz, welches kein striktes Naturgesetz ist, sondern eher ein Erklärungsversuch in der Natur und in der Gesellschaft vorkommende Zahlenmuster vorherzusagen.

Das Benfordsche Gesetz beruht auf der Tatsache, dass die Ziffern in einem Zahlensystem hierarchisch aufeinander aufbauen: Es beginnt mit der 1, dann folgt die 2, dann die 3 usw. In Kombination mit bestimmten Gesetzen der Natur (der natürliche Wachstumsprozess, dabei möglichst energiesparend wachsen/überleben) oder Ökonomie (so günstig wie möglich einkaufen) ist gemäß des Benfordschen Gesetz zu erwarten, dass die Ziffer 1 häufiger vorkommt als die 2, die wiederum häufiger vorkommt als die 3. Die Ziffer 9 braucht demnach den längsten Weg und kommt entsprechend verhältnismäßig seltener vor.

Dieses Phönomen hilft uns bei echten Zufallszahlen nicht weiter, denn dann sind alle Ziffern nicht aufeinander aufbauend, sondern mehr oder weniger gleichberechtigt in ihrem Auftrauen. Bei der klassischen und axiomatischen Wahrscheinlichkeit kommen wir damit also nicht ans Ziel.

Die Benford-Analyse ist im Grunde eine Ausreißeranalyse: Wir vergleichen Ziffernmuster in Datenbeständen mit der Erwartungshaltung des Benfordschen Gesetzes. Weicht das Muster von dieser Erwartung ab, haben wir Diskussionsbedarf.

Moderne Zahlensysteme sind Stellenwert-Zahlensysteme. Neben den Dual-, Oktal- und Hexadezimalzahlensystemen, mit denen sich eigentlich nur Informatiker befassen, wird unser Alltag vom Dezimalzahlensystem geprägt. In diesem Zahlensystem hat jede Stelle die Basis 10 (“dezi”) und einen Exponenten entsprechend des Stellenwertes, multipliziert mit der Ziffer d. Es ist eine Exponentialfunktion, die den Wert der Ziffern in bestimmter Reihenfolge ermittelt:

$Z =\sum_{i=-n}^{m}d_{i}\cdot10^{i}$

Die Benford-Analyse wird meistens nur für die erste Ziffer (also höchster Stellenwert!) durchgeführt. Dies werden wir gleich einmal beispielhaft umsetzen.

Die Wahrscheinlichkeit des Auftretens der ersten “anführenden” Ziffer d ist ein Logarithmus zur Basis B. Da wir im alltäglichen Leben – wie gesagt – nur im Dezimalzahlensystem arbeiten, ist für uns B = 10.

$p(d)=\log_{B}\left( 1 +\frac{1}{d} \right)$

Im Standard-Python lässt sich diese Formel leicht mit einer Schleife umsetzen:

1

2

3

4

5

import math

[round(math.log10(1+1/float(i))*100.0, 2) for i in range(1,10)]

Out: [30.1, 17.61, 12.49, 9.69, 7.92, 6.69, 5.8, 5.12, 4.58]

Benford-Algorithmus in Python mit NumPy und Pandas

Nachfolgend setzen wir eine Benford-Analyse als Minimalbeispiel in NumPy und Pandas um.

1

2

3

4

5

6

7

8

9

10

import numpy as np

x = np.arange(1,10) # NumPy-Array erstellen

x

Out: array([ 1, 2, 3, 4, 5, 6, 7, 8, 9])

benford = np.round(np.log10(1+1/x) * 100.0, decimals=2) # Den Logarithmus auf das NumPy-Array anwenden und runden

Out: array([ 30.1 , 17.61, 12.49, 9.69, 7.92, 6.69, 5.8 , 5.12,

4.58])

Nun möchten wir eine Tabelle erstellen, mit zwei Spalten, eine für die Ziffer (Digit), die andere für die relative Häufigkeit der Ziffer (Benford Law). Dazu nutzen wir das DataFrame aus dem Pandas-Paket. Das DataFrame erstellen wir aus den zwei zuvor erstellten NumPy-Arrays.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

import pandas as pd

benfordFrame = pd.DataFrame({'Digit': x, 'Benford Law': benford})

benfordFrame

Out:

Benford Law Digit

0 30.10 1

1 17.61 2

2 12.49 3

3 9.69 4

4 7.92 5

5 6.69 6

6 5.80 7

7 5.12 8

8 4.58 9

Man könnte sicherlich auch den natürlichen Index des DataFrames nutzen, indem wir diesen nur um jeweils 1 erhöhen, aber das verwirrt später nur und tun wir uns jetzt daher lieber nicht an…

1 2	benfordFrame.plot('Digit', 'Benford Law', kind='bar', title='Benford', legend=False)

Das Dataframe-Objekt kann direkt plotten (das läuft über die matplotlib, die wir aber nicht direkt einbinden müssen):

Diese neun Balken zeigen die Verteilung der Ziffernhäufigkeit nach dem Benfordschen Gesetz, diese Verteilung ist unsere Erwartungshaltung an andere nummerische Datenbestände, wenn diese einem natürlichen Wachstum unterliegen.

Analyse der Verteilung der ersten Ziffer in Zahlungsdaten

Jetzt brauchen wir Daten mit nummerischen Beträgen, die wir nach Benford testen möchten. Für dieses Beispiel nehme ich aus einem ein SAP-Testdatensatz die Spalte ‘DMBTR’ der Tabelle ‘BSEG’ (SAP FI). Die Spalte ‘DMBTR’ steht für “Betrag in Hauswährung’, die ‘BSEG’ ist die Tabelle für die buchhalterischen Belegsegmente.
Die Datei mit den Testdaten ist über diesen Link zum Download verfügbar (Klick) und enthält 40.000 Beträge.

Wir laden den Inhalt der Datei via NumPy.LoadTxt() und machen aus dem resultierenden NumPy-Array wieder ein Pandas.DataFrame und holen uns die jeweils erste Ziffer für alle Einträge als Liste zurück.

1

2

3

4

5

6

financialTransactions = np.loadtxt("[DEIN LOKALER PFAD]\\BSEG_DMBTR.csv", skiprows=1)

financialTransactionsFrame = pd.DataFrame({'Zahlungen':financialTransactions})

firstDigits = [str(value)[0:1] for value in financialTransactionsFrame['Zahlungen']]

Die Einträge der ersten Ziffer in firstDigits nehmen wir uns dann vor und gruppieren diese über die Ziffer und ihrer Anzahl relativ zur Gesamtanzahl an Einträgen.

1

2

3

4

5

percentDigits = np.asarray([[i, firstDigits.count(str(i))/float(len(financialTransactionsFrame['Zahlungen']))*100] for i in range(1, 10)])

percentDigits.T[1].sum()

Out: 94.0

Wenn wir die Werte der relativen Anzahl aufsummieren, landen wir bei 94% statt 100%. Dies liegt daran, dass wir die Ziffer 0 ausgelassen haben, diese jedoch tatsächlich vorkommt, jedoch nur bei Beträgen kleiner 1.00. Daher lassen wir die Ziffer 0 außenvor. Wer jedoch mehr als nur die erste Ziffer prüfen möchte, wird die Ziffer 0 wieder mit in die Betrachtung nehmen wollen. Nur zur Probe nocheinmal mit der Ziffer 0, so kommen wir auf die 100% der aufsummierten relativen Häufigkeiten:

1

2

3

4

percentDigits = np.asarray([[i, firstDigits.count(str(i))/float(len(financialTransactionsFrame['Zahlungen']))*100] for i in range(0, 10)])

percentDigits.T[1].sum()

Out: 100.0

Nun erstellen wir ein weiteres Pandas.DataFrame, mit zwei Spalten: Die Ziffern (Digit) und die tatsächliche Häufigkeit in der Gesamtpopulation (Real Distribution):

1 2	percentDigitsFrame = pd.DataFrame({'Digit':percentDigits[:,0], 'Real Distribution':percentDigits[:,1]})

Abgleich der Ziffernhäufigkeit mit der Erwartung

Nun bringen wir die theoretische Verteilung der Ziffern, also nach dem zuvor genannten Logarithmus, und die tatsächliche Verteilung der ersten Ziffern in unseren Zahlungsdaten in einem Plot zusammen:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

import matplotlib.pyplot as pyplot

fig = pyplot.figure()

ax = fig.add_subplot(111)

ax2 = ax.twinx()

percentDigitsFrame.plot('Digit', 'Real Distribution', kind='bar', ax=ax2, width = 0.4, color="green", position=0, legend=False)

benfordFrame.plot('Digit', 'Benford Law', kind='bar', ax=ax, width = 0.4, color="blue", position=1, legend=False)

lines, labels = ax.get_legend_handles_labels()

lines2, labels2 = ax2.get_legend_handles_labels()

ax2.legend(lines + lines2, labels + labels2, loc=0)

ax.set_ylim(1,35)

ax2.set_ylim(1,35)

pyplot.show()

In dem Plot wird deutlich, dass die Verteilung der führenden Ziffer in unseren Zahlungsdaten in ziemlich genau unserer Erwartung nach dem Benfordschen Gesetz entspricht. Es sind keine außerordentlichen Ausreißer erkennbar. Das wäre auch absolut nicht zu erwarten gewesen, denn der Datensatz ist mit 40.000 Einträgen umfassend genug, um dieses Muster gut abbilden zu können und von einer Manipulation dieser Beträge im SAP ist ebenfalls nicht auszugehen.

Gegenüberstellung: Computer-generierte Zufallszahlen

Jetzt wollen wir nochmal kurz darauf zurück kommen, dass das Benfordsche Gesetz für Zufallszahlen nicht unwendbar ist. Bei echten Zufallszahlen bin ich mir da auch sehr sicher. Echte Zufallszahlen ergeben sich beispielweise beim Lotto, wenn die Bälle mit Einzel-Ziffern durch eine Drehkugel hüpfen. Die Lottozahl-Ermittlung erfolgt durch die Zusammenstellung von jeweils gleichberechtigt erzeugten Ziffern.
Doch wie ist dies bei vom Computer generierten Zufallszahlen? Immerhin heißt es in der Informatik, dass ein Computer im Grunde keine Zufallszahlen erzeugen kann, sondern diese via Takt und Zeit erzeugt und dann durchmischt. Wir “faken” unsere Zahlungsdaten nun einfach mal via Zufallszahlen. Hierzu erstellen wir in NumPy ein Array mit 2000 Einträgen einer Zufallszahl (NumPy.Random.rand(), erzeugt floats 0.xxxxxxxx) und multiplizieren diese mit einem zufälligen Integer (Random.randint()) zwischen 0 und 1000.

1

2

3

from random import randint

financialTransactions = np.round(np.random.rand(2000) * randint(0,1000),decimals=2) # Zufallszahlen erzeugen, die auf dem ersten Blick als Zahlungsdaten durchgehen :-)

Erzeugen wir die obigen Datenstrukturen erneut, zeigt sich, dass die Verteilung der Zufallszahlen ganz anders aussieht: (vier unterschiedliche Durchläufe)

Anwendung in der Praxis

Data Scientists machen sich das Benfordsche Gesetz zu Nutze, um Auffälligkeiten in Zahlen aufzuspüren. In der Wirtschaftsprüfung und Forensik ist diese Analyse-Methode recht beliebt, um sich einen Eindruck von nummerischen Daten zu verschaffen, insbesondere von Finanztransaktionen. Die Auffälligkeit durch Abweichung vom Benfordchen Gesetz entsteht z. B. dadurch, dass Menschen eine unbewusste Vorliebe für bestimmte Ziffern oder Zahlen haben. Greifen Menschen also in “natürliche” Daten massenhaft (z. B. durch Copy&Paste) ein, ist es wahrscheinlich, dass sie damit auch vom Muster des Benfordschen Gesetzes abweichen. Weicht das Muster in Zahlungsströmen vom Bendfordsche Erwartungsmuster für bestimmte Ziffern signifikant ab, könnte dies auf Fälle von unnatürlichen Eingriffen hindeuten.

Die Benford-Analyse wird auch gerne eingesetzt, um Datenfälschungen in wissenschaftlichen Arbeiten oder Bilanzfälschungen aufzudecken. Die Benford-Analyse ist dabei jedoch kein Beweis, sondern liefert nur die Indizien, die Detailanalysen nach sich ziehen können/müssen.

Statistical Relational Learning

August 17, 2016/7 Comments/in Artificial Intelligence, Data Science, Machine Learning, Statistics /by Vishal Bhalla

An Introduction to Statistical Relational Learning – Part 1

Statistical Relational Learning (SRL) is an emerging field and one that is taking centre stage in the Data Science age. Big Data has been one of the primary reasons for the continued prominence of this relational learning approach given, the voluminous amount of data available now to learn interesting and unknown patterns from data. Moreover, the tools have also improved their processing prowess especially, in terms of scalability.

This introductory blog is a prelude on SRL and later on I would also touch base on more advanced topics, specifically Markov Logic Networks (MLN). To start off, let’s look at how SRL fits into one of the 5 different Machine Learning paradigms.

Five Machine Learning Paradigms

Lets look at the 5 Machine Learning Paradigms: Each of which is inspired by ideas from a different field!

Connectionists as they are called and led by Geoffrey Hinton (University of Toronto & Google and one of the major names in the Deep Learning community) think that a learning algorithm should mimic the brain! After all it is the brain that does all the complex actions for us and, this idea stems from Neuroscience.
Another group of Evolutionists whose leader is the late John Holland (from the University of Michigan) believed it is not the brain but evolution that was precedent and hence the master algorithm to build anything. And using this approach of having the fittest ones program the future they are currently building 3D prints of future robots.
Another thought stems from Philosophy where Analogists like Douglas R. Hofstadter an American writer and author of popular and award winning book – Gödel, Escher, Bach: an Eternal Golden Braid believe that Analogy is the core of Cognition.
Symbolists like Stephen Muggleton (Imperial College London) think Psychology is the base and by developing Rules in deductive reasoning they built Adam – a robot scientist at the University of Manchester!
Lastly we have a school of thought which has its foundations rested on Statistics & Logic, which is the focal point of interest in this blog. This emerging field has started to gain prominence with the invention of Bayesian networks 2011 by Judea Pearl (University of California Los Angeles – UCLA) who was awarded with the Turing award (the highest award in Computer Science). Bayesians as they are called, are the most fanatical of the lot as they think everything can be represented by the Bayes theorem using hypothesis which can be updated based on new evidence.

SRL fits into the last paradigm of Statistics and Logic. As such it offers another alternative to the now booming Deep Learning approach inspired from Neuroscience.

Background

In many real world scenario and use cases, often the underlying data is assumed to be independent and identically distributed (i.i.d.). However, real world data is not and instead consists of many relationships. SRL as such attempts to represent, model, and learn in the relational domain!

There are 4 main Models in SRL

Probabilistic Relational Models (PRM)
Markov Logic Networks (MLN)
Relational Dependency Networks (RDN)
Bayesian Logic Programs (BLP)

It is difficult to cover all major models and hence the focus of this blog is only on the emerging field of Markov Logic Networks.
MLN is a powerful framework that combines statistics (i.e. it uses Markov Random Fields) and logical reasoning (first order logic).

Academia

Some of the prominent names in academic and the research community in MLN include:

Professor Pedro Domingos from the University of Washington is credited with introducing MLN in his paper from 2006. His group created the tool called Alchemy which was one of the first, First Order Logic tools.
Another famous name – Professor Luc De Raedt from the AI group at University of Leuven in Belgium, and their team created the tool ProbLog which also has a Python Wrapper.
HAZY Project (Stanford University) led by Prof. Christopher Ré from the InfoLab is doing active research in this field and Tuffy, Felix, Elementary, Deep Dive are some of the tools developed by them. More on it later!
Talking about academia close by i.e. in Germany, Prof. Michael Beetz and his entire team moved from TUM to TU Bremen. Their group invented the tool – ProbCog
At present, Prof. Volker Tresp from Ludwig Maximilians University (LMU), Munich & Dr. Matthias Nickles at Technical University of Munich (TUM) have research interests in SRL.

Theory & Formulation

A look at some background and theoretical concepts to understand MLN better.

A. Basics – Probabilistic Graphical Models (PGM)

The definition of a PGM goes as such:

A PGM encodes a joint p(x,y) or conditional p(y|x) probability distribution such that given some observations we are provided with a full probability distribution over all feasible solutions.

A PGM helps to encode relationships between a set of random variables. And it achieves this by making use of a graph! These graphs can be either be Directed or Undirected Graphs.

B. Markov Blanket

A Markov Blanket is a Directed Acyclic graph. It is a Bayesian network and as you can see the central node A highlighted in red is dependent on its parents and parents of descendents (moralization) by the circle drawn around it. Thus these nodes are the only knowledge needed to predict node A.

Image courtesy – Wikipedia

C. Markov Random Fields (MRF)

A MRF is an Undirected graphical model. Every node in an MRF satisfies the Local Markov property of Conditional Independence, i.e. a node is conditionally independent of another node, given its neighbours. And now relating it to Markov Blanket as explained previously, a Markov blanket for a node is simply its adjacent nodes!

Image courtesy – Wikipedia

Intuition

We now that Probability handles uncertainty whereas Logic handles complexity. So why not make use of both of them to model relationships in data that is both uncertain and complex. Markov Logic Networks (MLN) precisely does that for us!

MLN is composed of a set of pairs of <w, F> where F is the formula (written in FO logic) and weights (real numbers identifying the strength of the constraint).

MLN basically provides a template to ground a Markov network. Grounding would be explained in detail in the next but one section on “Weight Learning”.

It can be defined as a Log linear model where probability of a world is given by the weighted sum of all true groundings of a formula i under an exponential function. It is then divided by Z which is termed as the partition function and used to normalize and get probability values between 0 and 1.

The MLN Template

Rules or Predicates

The relation to be learned is expressed in FO logic. Some of the different possible FO logical connectives and quantifiers are And (^), Or (V), Implication (→), and many more. Plus, Formulas may contain one or more predicates, connected to each other with logical connectives and quantified symbols.

Evidence

Evidence represent known facts i.e. the ground predicates. Each fact is expressed with predicates that contain only constants from their corresponding domains.

Weight Learning

Discover the importance of relations based on grounded evidence.

Inference

Query relations, given partial evidence to infer a probabilistic estimate of the world.

More on Weight Learning and Inference in the next part of this series!

Hope you enjoyed the read. I have deliberately kept the content basic and a mix of non technical and technical so as to highlight first the key players and some background concepts and generate the reader’s interest in this topic, the technicalities of which can easily be read in the paper. Any feedback as a comment below or through a message are more than welcome!

Continue reading with Statistical Relational Learning – Part II.

References

Richardson, Matthew, and Pedro Domingos – Markov logic networks. In Machine learning, vol. 62, no. 1-2, pp. 107-136, 2006.
Pedro’s TEDx video at University of Washington: The Quest for the Master Algorithm
Hazy project webpage

Einführung in WEKA

July 20, 2016/1 Comment/in Business Analytics, Business Intelligence, Data Mining, Data Science, Main Category, Statistics, Tool Introduction, Tutorial, Visualization /by Victoria Ivanova

Waikato Environment for Knowledge Analysis, kurz WEKA, ist ein quelloﬀenes, umfangreiches, plattformunabhängiges Data Mining Softwarepaket. WEKA ist in Java geschrieben und wurde an der WAIKATO Iniversität entwickelt. In WEKA sind viele wichtige Data Mining/Machine Learning Algorithmen implementiert und es gibt extra Pakete, wie z. B. LibSVM für Support Vector Machines, welches nicht in WEKA direkt implementiert wurde. Alle Einzelheiten zum Installieren und entsprechende Download-Links ﬁndet man unter auf der Webseite der Waikato Universität. Zusammen mit der Software wird ein Manual und ein Ordner mit Beispiel-Datensätzen ausgeliefert. WEKA arbeitet mit Datensätzen im sogenannten attribute-relation file format, abgekürzt arﬀ. Das CSV-Format wird aber ebenfalls unterstützt. Eine Datei im arﬀ-Format ist eine ASCI-Textdatei, welche aus einem Header- und einem Datateil besteht. Im Header muss der Name der Relation und der Attribute zusammen mit dem Typ stehen, der Datenteil beginnt mit einem @data-Schlüsselwort. Als Beispiel sei hier ein Datensatz mit zwei Attributen und nur zwei Instanzen gegeben.

1

2

3

4

5

6

7

@relation my_relation

@attribute first_attribute numeric

@attribute second_attribute numeric

@attribute class {-1,1}

@data

2.5 3.8 1

1.2 1.5 -1

WEKA unterstützt auch direktes Einlesen von Daten aus einer Datenbank (mit JDBC) oder URL. Sobald das Tool installiert und gestartet ist, landet man im Hauptmenü von WEKA – WEKA GUI Chooser 1.

Abbildung 1: WEKA GUI Chooser

Der GUI Chooser bietet den Einstieg in WEKA Interfaces Explorer, Experimenter, KnowledgeFlow und simple CLI an. Der Explorer ist ein graphisches Interface zum Bearbeiten von Datensätzen, Ausführen von Algorithmen und Visualisieren von den Resultaten. Es ist ratsam, dieses Interface als Erstes zu betrachten, wenn man in WEKA einsteigen möchte. Beispielhaft führen wir jetzt ein paar Algorithmen im Explorer durch.

Der Explorer bietet mehrere Tabs an: Preprocess, Classify, Cluster, Associate, Select attributes und Visualize. Im Preprocess Tab hat man die Möglichkeit Datensätze vorzubereiten. Hier sind zahlreiche Filter zum Präprozessieren von Datensätzen enthalten. Alle Filter sind in supervised und unsupervised unterteilt, je nachdem, ob das Klassenattribut mitbetrachtet werden soll oder nicht. Außerdem kann man entweder Attribute oder Instanzen betrachten, mit Attributen lässt man Filter spaltenweise arbeiten und bei Instanzen reihenweise. Die Auswahl der Filter ist groß, man kann den ausgewählten Datensatz diskretisieren, normalisieren, Rauschen hinzufügen etc. Unter Visualize können z. B. die geladenen Datensätze visualisert werden. Mit Select attributes kann man mithilfe von Attribut Evaluator und Search Method ein genaueres Ergebnis erzielen. Wenn man im Preprocess den Datensatz lädt, erhält man einen Überblick über den Datensatz und dessen Visualisierung. Als Beispiel wird hier der Datensatz diabetes.arﬀ genommen, welcher mit WEKA zusammen ausgeliefert wird. Dieser Datensatz enthält 768 Instanzen mit je 9 Attributen, wobei ein Attribut das Klassenattribut ist. Die Attribute enthalten z. B. Informationen über die Anzahl der Schwangerschaften, diastolischer Blutdruck, BMI usw. Alle Attribute, außer dem Klassenattribut, sind numerisch. Es gibt zwei Klassen tested negativ und tested positiv, welche das Resultat des Testens auf diabetes mellitus darstellen. über Preprocess -> Open File lädt man den Datensatz in WEKA und sieht alle relevanten Informationen wie z. B. Anzahl und Name der Attribute. Nach dem Laden kann der Datensatz klassiﬁziert werden.

Abbildung 2: Diabetes.arﬀ Datensatz geladen in WEKA

Hierzu einfach auf Classify klicken und unter Choose den gewünschten Algorithmus auswählen. Für diesen Datensatz wählen wir jetzt den Algorithmus kNN (k-Nearest Neighbour). Der Algorithmus klassiﬁziert das Testobjekt anhand der Klassenzugehörigkeit von den k Nachbarobjekten, die am nähsten zu dem Testobjekt liegen. Die Distanz zwischen den Objekten und dem Testobjekt wird mit einer Ähnlichkeitsmetrik bestimmt, meistens als euklidische oder Manhattan-Distanz. In WEKA ist der Algorithmus unter lazy iBk zu ﬁnden. Wenn man auf das Feld neben dem Algorithmusnamen in WEKA mit rechter Maustaste klickt, kann man unter show properties die Werte für den ausgewählten Algorithmus ändern, bei iBk kann man u.A. den Wert für k ändern. Für den ausgewählten Datensatz diabetes.arﬀ stellen wir beispielsweise k = 3 ein und führen die 10-fache Kreuzvalidierung durch, indem wir unter Test Options die Cross Validation auswählen. Nach der Klassiﬁkation werden die Ergebnisse in einer Warhheitsmatrix präsentiert. In unserem Fall sieht diese wie folgt aus:

1

2

3

a b <-- classified as

410 90 | a = tested_negative

120 148 | b = tested_positive

Die Anzahl der richtig klassiﬁzierten Instanzen beträgt 72.6563 %. Wenn man in der Result list auf den entsprechenden Algorithmus einen Rechtsklick macht, kann man z. B. noch den Fehler der Klassiﬁzierung visualisieren. Entsprechend lassen sich im Explorer unter Cluster Clustering-Algorithmen und unter Associate Assoziationsalgorithmen auf einen ausgewählten Datensatz anwenden. Die restlichen Interfaces von WEKA bieten z. T. die gleiche Funktionalität oder erweitern die Möglichkeiten des Experimentierens, fordern aber mehr Erfahrung und Wissen von dem User. Das Experimenter Interface dient dazu, mehrere Datensätze mit mehreren Algorithmen zu analysieren. Mit diesem Interface kann man groß-skalierte Experimente durchführen. Simple CLI bietet dem User eine Kommandozeile, statt einem graphischen Interface, an.

Toolkits & Services für Semantische Textanalysen

March 16, 2016/0 Comments/in Big Data, Data Mining, Data Science Hack, Data Science News, Machine Learning, Main Category, Statistics, Text Mining, Tool Introduction, Tools /by Dr. Dietrich Wettschereck

Named Entity Recognition ist ein Teilgebiet von Information Extraction. Ziel von Information Extraction ist die Gewinnung semantischer Informationen aus Texten (im Gegensatz zum verwandten Gebiet des Information Retrieval, bei dem es um das möglichst intelligente Finden von Informationen, die u.U. vorab mit Information Extraction gewonnen wurden, geht). Named Entity Recognition (kurz NER) bezeichnet die Erkennung von Entitäten wie z.B. Personen, Organisationen oder Orten in Texten.

[box]Beispiel:
“Albert Einstein war ein theoretischer Physiker, der am 14. März 1879 in Ulm geboren wurde. Er erhielt 1921 den Nobelpreis für Physik. Isaac Newton, Einstein und Stephen Hawking werden oft als die größten Physiker seit der Antike bezeichnet.”[/box]

Die Disambiguierung von Entitäten ist ein weiterer wichtiger Schritt auf dem Weg zu einem semantischen Verständnis von Texten. Wenn man so in obigem Text erkennen kann, dass “Albert Einstein“, “Er” und “Einstein” die gleiche Person bezeichnen, so kann ein Analyseverfahren z.B. daraus schließen, dass in diesem Text Einstein eine wichtigere Rolle spielt, als Newton, der nur einmal erwähnt wurde. Die Hyperlinks hinter den jeweiligen Entitäten zeigen eine Möglichkeit der semantischen Anreicherung von Texten an – in diesem Fall wurden die Entitäten mit entsprechenden Einträgen bei DBpedia automatisch verlinkt.

Named Entity Recognition dient vorrangig zwei Zwecken:

Anreicherung von Texten mit Metadaten
Abstraktion von Texten zur besseren Erkennung von Mustern

Punkt 1 dient direkt dem Information Retrieval. Anwender können so z.B. gezielt nach bestimmten Personen suchen, ohne alle möglichen Schreibweisen oder Berufsbezeichnungen auflisten zu müssen.

Punkt 2 dient der Vorverarbeitung von Texten als Input für Machine Learning Verfahren. So ist es (je nach Anwendung!) oft nicht von Bedeutung, welche Person, welcher Ort oder auch welche Uhrzeit in einem Text steht sondern nur die Tatsache, dass Personen, Orte oder Zeiten erwähnt wurden.

Sirrus Shakeri veranschaulicht die zentrale Bedeutung semantischer Analyse in seinem Beitrag From Big Data to Intelligent Applications:

Abbildung 1: Von Big Data zu Intelligent Applications von Cirrus Shakeri

Sein “Semantic Graph” setzt voraus, dass Entitäten mittels “Natural Language Processing” erkannt und zueinander in Beziehung gesetzt wurden.

Es ist interessant zu vermerken, dass Natural Language Processing und Data Mining / Machine Learning über viele Jahre als Alternativen zueinander und nicht als Ergänzungen voneinander gesehen wurden. In der Tat springen die meisten Vorgehensmodelle heutzutage von “Data Preparation” zu “Machine Reasoning”. Wir argumentieren, dass sich in vielen Anwendungen, die auf unstrukturierten Daten basieren, signifikante Qualitätsverbesserungen erzielen lassen, wenn man zumindest NER (inklusive Disambiguierung) in die Pipeline mit einbezieht.

Toolkits und Services für NER

Es existiert eine Vielzahl von Toolkits für Natural Language Processing, die Sie mehr oder weniger direkt in Ihre Programme einbinden können. Exemplarisch seien drei Toolkits für Java, Python und R erwähnt:

Der Stanford Named Entity Recognizer (Java) ist Teil eines mächtigen NLP Toolkits, das an der Stanford University entwickelt wurde. Es gibt neben anderen Sprachen auch vortrainierte Modelle für Deutsch.
Das Natural Language Toolkit (Python) ist ein typisches Open Source Community Projekt mit hunderten von Erweiterungen und Modellen für NLP.
Auch für R-User gibt es entsprechende Packages z.B. die R NLP Package (siehe auch https://rpubs.com/lmullen/nlp-chapter für weitere Hinweise)

Diese Toolkits enthalten Modelle, die auf Korpora für die jeweils unterstützten Sprachen trainiert wurden. Sie haben den Vorteil, dass sie auch vollkommen neue Entitäten erkennen können (wie z.B. neue Politiker oder Fernsehstars, die zur Trainingszeit noch unbekannt waren). Je nach Einstellung haben diese Systeme aber auch eine relativ hohe Falsch-Positiv-Rate.

Wer NER nur ausprobieren möchte oder lediglich gelegentlich kleinere Texte zu annotieren hat, sei auf die folgenden Web Services verwiesen, die auch jeweils eine REST-Schnittstelle anbieten.

DBpedia

Das DBpedia Projekt nutzt die strukturierten Informationen der verschieden-sprachigen Wikipedia Sites für den Spotlight Service. Im Unterschied zu den reinen Toolkits nutzen die nun genannten Werkzeuge zusätzlich zu den trainierten Modellen eine Wissensbasis zur Verringerung der Falsch-Positiv-Rate. Die mehrsprachige Version unter http://dbpedia-spotlight.github.io/demo zeigt die Möglichkeiten des Systems auf. Wählen Sie unter “Language” “German“) und dann über “SELECT TYPES…” die zu annotierenden Entitätstypen. Ein Beispieltext wird automatisch eingefügt. Sie können ihn natürlich durch beliebige andere Texte ersetzen. Im folgenden Beispiel wurden “Organisation”, “Person”, und “Place“ ausgewählt:

Abbildung 2: DBpedia Demo (de.dbpedia.org)

Die erkannten Entitäten werden direkt mit ihren DBpedia Datenbankeinträgen verlinkt. Im Beispiel wurden die Orte Berlin, Brandenburg und Preußen sowie die Organisationen Deutsches Reich, Deutsche Demokratische Republik, Deutscher Bundestag und Bundesrat erkannt. Personen wurden in dem Beispieltext nicht erkannt. Die Frage, ob man “Sitz des Bundespräsidenten” als Ort (Sitz), Organisation (das Amt des Bundespräsidenten) und / oder Person (der Bundespräsident) bezeichnen sollte, hängt durchaus vom Anwendungsszenario ab.

OpeNER

Das OpeNER Projekt ist das Ergebnis eines europäischen Forschungsprojekts und erweitert die Funktionalität von DBpedia Spotlight mit weiteren semantischen Analysen. Die Demo unter http://demo2-opener.rhcloud.com/welcome.action (Tab “Live Analysis Demo“, “Named Entity Recognition and Classification” und “Named Entity Linking” auswählen und “Analyse” drücken, dann auf der rechten Seite das Tab “NERC” anwählen) ergibt für den gleichen Beispieltext:

Abbildung 3: OpeNER Projekt (opener-project.eu)

Organisationen sind blau hinterlegt, während Orte orange markiert werden. Auch hier werden erkannte Entitäten mit ihren DBpedia Datenbankeinträgen verknüpft. Die Bedeutung dieser Verknüpfung erkennt man wenn man auf das Tab “Map” wechselt. Berlin wurde als Ort erkannt und über die Geo-Koordinaten (geo:long = 13.4083, geo.lat = 52.5186) im DBpedia Eintrag von Berlin konnte das Wort “Berlin” aus obigem Text automatisch auf der Weltkarte referenziert werden.

Es gibt eine Vielzahl weiterer Services für NLP wie z.B. OpenCalais. Einige dieser Services bieten bestimmte Funktionalitäten (wie z.B. Sentiment Analysis) oder andere Sprachen neben Englisch nur gegen eine Gebühr an.

Listen Tagger

Der Vollständigkeit halber sei noch erwähnt, dass in den meisten Anwendungsszenarien die oben genannten Werkzeuge durch sogenannte Listen-Tagger (englisch Dictionary Tagger) ergänzt werden. Diese Tagger verwenden Listen von Personen, Organisationen oder auch Marken, Bauteilen, Produktbezeichnern oder beliebigen anderen Gruppen von Entitäten. Listen-Tagger arbeiten entweder unabhängig von den oben genannten statistischen Taggern (wie z.B. dem Standford Tagger) oder nachgeschaltet. Im ersten Fall markieren diese Tagger alle Vorkommen bestimmter Worte im Text (z.B. „Zalando“ kann so direkt als Modemarke erkannt werden). Im zweiten Fall werden die Listen genutzt, um die statistisch erkannten Entitäten zu verifizieren. So könnte z.B. der Vorschlag des statistischen Taggers automatisch akzeptiert werden wenn die vorgeschlagene Person auch in der Liste gefunden wird. Ist die Person jedoch noch nicht in der Liste enthalten, dann könnte ein Mitarbeiter gebeten werden, diesen Vorschlag zu bestätigen oder zu verwerfen. Im Falle einer Bestätigung wird die neu erkannte Person dann in die Personenliste aufgenommen während sie im Falle einer Ablehnung in eine Negativliste übernommen werden könnte damit dieser Vorschlag in Zukunft automatisch unterdrückt wird.

Regular Expression Tagger

Manche Entitätstypen folgen klaren Mustern und können mit hoher Zuverlässigkeit durch reguläre Ausdrücke erkannt werden. Hierzu zählen z.B. Kreditkarten- oder Telefon- oder Versicherungsnummern aber auch in vielen Fällen Bauteilbezeichner oder andere firmeninterne Identifikatoren.

Fazit

Natural Language Processing und insbesondere Named Entity Recognition und Disambiguierung sollte Teil der Werkzeugkiste eines jeden Anwenders bei der Analyse von unstrukturierten Daten sein. Es existieren mehrere mächtige Toolkits und Services, die allerdings je nach Anwendungsgebiet kombiniert und verfeinert werden müssen. So erkennt DBpedia Spotlight nur Entitäten, die auch einen Wikipedia Eintrag haben, kann für diese aber reichhaltige Metadaten liefern. Der Stanford Tagger hingegen kann auch vollkommen unbekannte Personennamen aus dem textuellen Kontext erkennen, hat aber bei manchen Texten eine relativ hohe Falsch-Positiv-Rate. Eine Kombination der beiden Technologien und anwendungsspezifischen Listen von Entitäten kann daher zu qualitativ sehr hochwertigen Ergebnissen führen.

MLN Template – explained

Weight Learning

Weight Learning – An Example

Inference

Inference – An Example

Tool-kits

Die ersten Schritte

Neue Variablen

Aggregate

Daten in Reih’ und Glied

Fazit und Ausblick

Die Vorarbeit

ABC – Analyse:

Klassifikation:

XYZ – Analyse

Klassifikation:

ABC-XYZ-Analyse

Was ist die Warenkorbanalyse?

Datenaufbau

Beschreibende Datenanalyse

Verbundanalyse

Assoziationsregeln

Algorithmen

Umsetzung mit R

Referenzen:

Benford-Algorithmus in Python mit NumPy und Pandas

Analyse der Verteilung der ersten Ziffer in Zahlungsdaten

Abgleich der Ziffernhäufigkeit mit der Erwartung

Gegenüberstellung: Computer-generierte Zufallszahlen

Anwendung in der Praxis

An Introduction to Statistical Relational Learning – Part 1

Toolkits und Services für NER

DBpedia

OpeNER

Listen Tagger

Regular Expression Tagger

Fazit

Interesting links

Pages

Categories

Archive