Perspektiv-Wechsel mit Process Mining
Data Scientists verbringen einen Großteil ihres Tages mit explorativer Analyse. In der 2015 Data Science Salary Survey[1] gaben 46% der Befragten an, ein bis drei Stunden pro Tag auf das Zusammenfassen, Visualisieren und Verstehen von Daten zu verwenden, mehr noch als auf die Datensäuberung und Datenaufbereitung.
Process Mining konzentriert sich auf die Analyse von Prozessen[2], und ist insbesondere für die explorative Analyse von prozessbezogenen Daten ein hervorragendes Werkzeug. Wenn sich Ihr Data-Science-Projekt auf Geschäfts- oder IT-Prozesse bezieht, dann müssen Sie diese Prozesse erst erforschen und genau verstehen, bevor Sie sinnvoll Machine-Learning Algorithmen trainieren oder statistische Analysen fahren können.
Mit Process Mining können Sie eine Prozess-Sicht auf die Daten einnehmen. Die konkrete Prozess-Sicht ergibt sich aus den folgenden drei Parametern:
- Case ID: Die gewählte Vorgangsnummer bestimmt den Umfang des Prozesses und verbindet die Schritte einer einzelne Prozessinstanz von Anfang bis Ende (z.B. eine Kundennummer, Bestellnummer oder Patienten-ID)
- Activity: Der Aktivitätsname bestimmt die Arbeitsschritte, die in der Prozesssicht dargestellt werden (z.B. „Bestellung empfangen“ oder „Röntgenuntersuchung durchgeführt“).
- Timestamp: Ein oder mehrere Zeitstempel pro Arbeitsschritt (z.B. vom Start und vom Ende der Röntgenuntersuchung) werden zur Berechnung der Prozessabfolge und zum Ableiten von parallelen Prozessschritten herangezogen.
Wenn Sie einen Datensatz mit Process Mining analysieren, dann bestimmen Sie zu Beginn der Analyse, welche Spalten in den Daten der Case ID, dem Aktivitätsnamen und den Timestamps entsprechen. Beim Import der Daten in das Process Mining Tool können Sie diese Parameter dann in der Konfiguration einstellen.
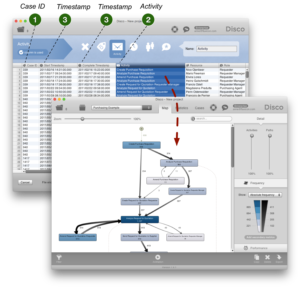
Beim Importieren einer CSV-Datei in die Process Mining Software Disco können Sie für jede Spalte in ihrem Datensatz auswählen, wie diese interpretiert werden soll.[a] In dem folgenden abgebildeten Beispiel eines Einkaufsprozesses sind die Case ID-Spalte (die Bestellnummer) als Case ID, die Start- und Complete-Timestamps als Timestamp und die Activity-Spalte als Activity eingestellt. Als Ergebnis produziert die Process Mining Software vollautomatisch eine grafische Darstellung des tatsächlichen Einkaufsprozesses auf Basis der historischen Daten. Der Prozess kann jetzt faktenbasiert weiter analysiert werden.
aFür die Open-Source-Software ProM arbeitet man oft über XML-Formate wie XES oder MXML, die diese Konfiguration abbilden.
In der Regel ergibt sich die erste Prozesssicht – und die daraus abzuleitende Import-Konfiguration – aus der Aufgabenstellung und dem Prozessverständnis.
Allerdings ist vielen Process-Mining-Neulingen noch nicht bewusst, dass eine große Stärke von Process Mining als exploratives Analyse-Werkzeug gerade darin besteht, dass man schnell und flexibel verschiedene Sichten auf den Prozess einnehmen kann. Die oben genannten Parameter funktionieren wie eine Linse, mit der Sie Prozesssichten aus verschiedenen Blickwinkeln einstellen können.
Hier sind drei Beispiele:
1. Anderer Aktivitäts-Fokus
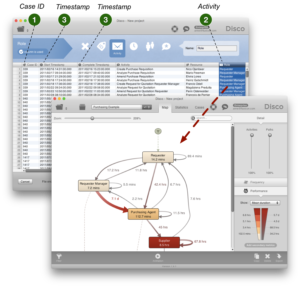
Für den obigen Einkaufsprozess können wir z.B. den Fokus auch auf den organisatorischen Übergabefluss richten, indem wir als Activity die Role-Spalte (die Funktion oder Abteilung des Mitarbeiters) einstellen.
Somit kann der gleiche Prozess (und sogar der gleiche Datensatz) nun aus der organisationalen Perspektive analysiert werden. Ping-Pong-Verhalten und erhöhte Wartezeiten bei der Übergabe von Vorgängen zwischen Abteilungen können sichtbar gemacht und adressiert werden.
2. Kombinierte Aktivität
Anstatt den Fokus zu wechseln können wir auch verschiedene Dimensionen kombinieren, um ein detaillierteres Bild von dem Prozess zu bekommen.
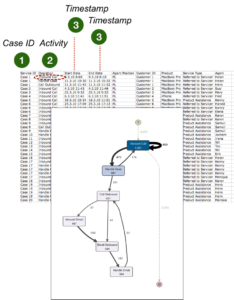
Wenn Sie sich den folgenden Callcenter-Prozess anschauen, dann würden Sie vermutlich zunächst die Spalte ‘Operation’ als Aktivitätsname einstellen. Als Ergebnis sehen wir den folgenden Prozess mit sechs verschiedenen Prozessschritten, die u.a. das Annehmen von eingehenden Kundenanrufen (‚Inbound Call’) und interne Aktivitäten (‚Handle Case’) repräsentieren.
Jetzt stellen Sie sich vor, dass Sie den Prozess gern genauer analysieren würden. Sie möchten gern sehen, wie oft eingehende Anrufe von dem First-Level Support im Callcenter an die Spezialisten im Backoffice weitergeleitet werden. Tatsächlich sind diese Informationen in den Daten enthalten. Das Attribut ‚Agent Position’ gibt an, ob die Aktivität im First-Level Support (als ‘FL’ vermerkt) oder im Backoffice (als ‘BL’ vermerkt) stattgefunden hat.
Um die ‚Agent Position’ in die Aktivitätssicht mitzunehmen, können wir einfach sowohl die Spalte ‘Operation’ als auch die Spalte ‘Agent Position’ als Aktivitätsnamen einstellen. Die Inhalte der beiden Spalten werden nun zusammengefasst (konkateniert).
Als Ergebnis bekommen wir eine detailliertere Sicht auf den Prozess. Wir sehen z.B., dass im First-Level Support angenommene Anrufe 152 mal an das Backoffice zur weiteren Verarbeitung übergeben wurden.
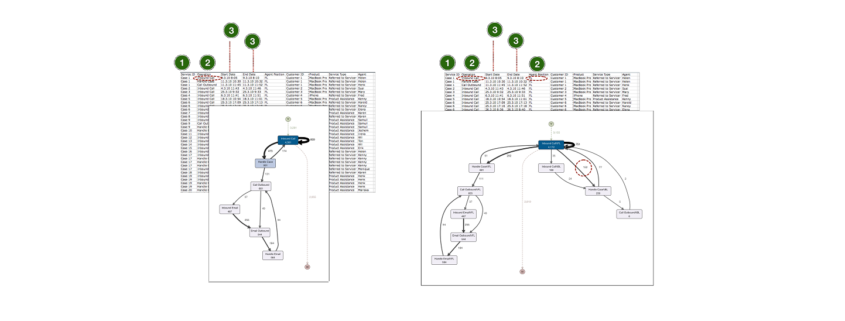
3. Alternativer Case-Fokus
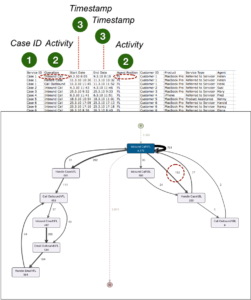
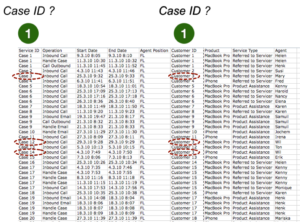
Zuletzt können wir für den gleichen Callcenter-Prozess in Frage stellen, ob die als Vorgangsnummer gewählte Service-Request-ID des CRM-Systems die gewünschte Prozesssicht bietet. Immerhin gibt es auch eine Kundennummer und für ‚Customer 3’ sind mindestens drei verschiedene Service-Anfragen vermerkt (Case 3, Case 12 und Case 14).
Was ist, wenn diese drei Anfragen zusammenhängen und sich die Service-Mitarbeiter nur nicht die Mühe gemacht haben, den bestehenden Case im System zu suchen und wieder zu öffnen? Das Ergebnis wäre eine verminderte Kundenzufriedenheit, weil der ‚Customer 3’ bei jedem Anruf erneut seine Problembeschreibung abgeben muss.
Das Ergebnis wäre außerdem eine geschönte ‚First Call Resolution Rate’: Die ‚First Call Resolution Rate’ ist eine typische Prozesskennzahl in Callcentern, in der gemessen wird, wie oft ein Kundenproblem im ersten Anruf gelöst werden konnte.
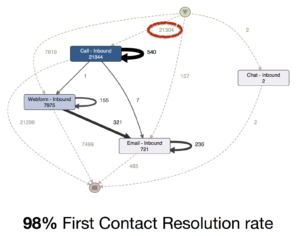
Genau das ist in dem Kundenservice-Prozess eines Internet-Unternehmens passiert[3]. In einem Process-Mining-Projekt wurde zunächst der Kontaktaufnahmeprozess (über Telefon, Internet, E-Mail oder Chat) über die Service ID als Vorgangsnummer analysiert. In dieser Sicht ergab sich eine beeindruckende ‚First Contact Resolution Rate’ von 98%. Unter 21.304 eingehenden Anrufen gab es scheinbar nur 540 Wiederholungsanrufe.
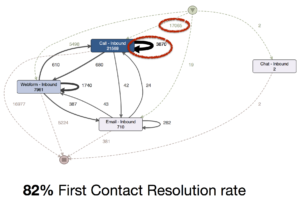
Dann fiel den Analysten auf, dass alle Service-Anfragen immer ziemlich schnell geschlossen und so gut wie nie wieder geöffnet wurden. Um den Prozess aus Kundenperspektive zu analysieren, verwendeten sie dann die Kundennummer als Case ID. Somit wurden alle Anrufe eines Kunden in dem Zeitraum zu einem Vorgang zusammengefasst und die Wiederholungsanrufe wurden sichtbar.
Die ‚First Contact Resolution Rate’ betrug in Wirklichkeit nur 82%. Nur 17.065 Fälle wurden in Wirklichkeit von einem eingehenden Anruf gestartet. Über 3000 waren Wiederholungsanrufe, die aber als neue Serviceanfragen im System (und im Performance-Report!) gezählt wurden.
Fazit
Process Mining ermöglicht es Ihnen eine Prozessperspektive auf Ihre Daten einzunehmen. Darüber hinaus lohnt es sich, verschiedene Sichten auf den Prozess zu betrachten. Halten Sie Ausschau nach anderen Aktivitäts-Perspektiven, möglichen Kombinationen von Feldern und neuen Sichtweisen darauf, was einen Vorgang im Prozess ausmacht.
Sie können verschiedene Blickwinkel einnehmen, um verschiedene Fragen zu beantworten. Oft ergeben erst verschiedene Sichten zusammen ein Gesamtbild auf den Prozess.
Möchten Sie die in diesem Artikel vorgestellten Perspektiv-Wechsel einmal selbst genauer erforschen? Sie können die verwendeten Beispiel-Dateien herunterladen (Zip-Verzeichnis) und direkt mit der frei verfügbaren Demo-Version unserer Process Mining Software Disco analysieren.
Quellen
[1] 2015 Data Science Salary Survey (von Oreilly.com, PDF)
[2] Komplexe Abläufe verständlich dargestellt mit Process Mining (hier im Data Science Blog)
[3] You Need To Be Careful How You Measure Your Processes (fluxicon.com)






 gif
gif