Wie lernen Maschinen?

Im dritten Teil meiner Reihe Wie lernen Maschinen? wollen wir die bisher kennengelernten Methoden anhand eines der bekanntesten Verfahren des Maschinellen Lernens – der Linearen Regression – einmal gegenüberstellen. Die Lineare Regression dient uns hier als Prototyp eines Verfahrens aus dem Gebiet der Regression, in weiteren Artikeln werden die Logistische Regression als Prototyp eines Verfahrens aus dem Gebiet der Klassifikation und eine Collaborative-Filtering- bzw. Matrix-Faktorisierungs-Methode als Prototyp eines Recommender-Systems behandelt.

Es ist bemerkenswert, dass sich alle drei Machine-Learning-Verfahren mit dem gleichen Optimierungsansatz trainieren lassen, d.h. die zugrundeliegende mathematische Behandlung ist in allen Fällen identisch, obwohl die Verfahren in ganz verschiedenen Anwendungsbereichen eingesetzt werden und darüberhinaus auch die Methodik und sogar die Natur der Inputdaten teilweise eine ganz andere ist. So sind beispielsweise bei Regressionsaufgaben alle Variablen – die abhängigen wie die unabhängigen – numerisch, während bei Klassifikationsaufgaben die abhängige Variable nicht-numerisch ist, hier werden üblicherweise Kategorien oder Klassen unterschieden, etwa die Typen A und B. Der verwendete R-Code lässt sich wieder im github-Repository anschauen und herunterladen.

Lineare Regression

Die Lineare Regression ist sicherlich eines der bekanntesten und am häufigsten verwendeten Verfahren im Bereich des Machine Learnings. Hierbei versucht man, einen linearen Zusammenhang zwischen einer oder mehrerer numerischer Features oder unabhängiger Variablen – repräsentiert durch $x_1,…,x_n$ – und einer ebenfalls numerischen abhängigen Variable $y$ zu bestimmen. Das Ziel ist, durch eine geeignete Linearkombination der $x_i$ dem zugehörigen $y$ möglichst nahe zu kommen. Wir formulieren dies erst einmal ganz allgemein und nehmen an, dass wir $m$ Zeilenvektoren oder

Datenpunkte: $x^{(j)}=[x^{(j)}_1,…x^{(j)}_n]$ , $j=1,…,m$

gegeben haben. Für jeden Datenpunkt gibt es einen zugehörigen

Zielwert: $y_j$ .

Der Ansatz der linearen Regression besteht nun darin, geeignete reellwertige Parameter $c_i$ , $i=0,1,…,n$ , zu finden, so dass für alle Datenpunkte $x^{(j)}$ und die jeweiligen $y_j$ gilt:

Ansatz als Linearkombination: $y_j \approx c_0 + c_1 x^{(j)}_1 + … + c_n x^{(j)}_n.$

Wir sammeln nun die $n+1$ Parameter $c_i$ im

Parametervektor: $c := [c_0,c_1,…,c_n]$

und – um der Konstante $c_0$ aus obiger Beschreibung der Linearen Regression Rechnung zu tragen – ergänzen wir jeden Datenpunkt um eine $1$ an Anfang, d.h. wir führen eine weitere unabhängige Variable $x_0$ ein der Form

“Konstante” Variable: $x_0 := [1,1,…,1]^T$

Nun können wir die unabhängigen Variablen $x_0,x_1,…,x_n$ als Spalten einer Matrix $X$ auffassen und erhalten in der aus der Linearen Algebra bekannten Matrix-Notation eine Art

Lineares Gleichungssystem: $Xc\approx y.$

Für gegebene Inputdaten $X$ und $y$ suchen wir nun also nach einer Lösung oder einem optimalen Parametervektor $c^*$ , so dass das obige lineare Gleichungssystem bestmöglich erfüllt ist. Im allgemeinen geht dies nämlich nicht exakt, insbesondere wenn die Anzahl $m$ der Datenpunkte die Anzahl $n+1$ der Variablen übersteigt. In diesem Fall nennt man das Gleichungssystem überbestimmt, die verschiedenen Gleichungen können sich gewissermaßen “widersprechen”, d.h. unter Umständen nicht alle gleichzeitig erfüllt sein. Dies führt uns zu der Frage, was genau bestmöglich in diesem Kontext bedeuten soll.

Die Zielfunktion für die Lineare Regression

Betrachten wir das obige Gleichungssystem, so sehen wir auf der linken und rechten Seite jeweils einen Vektor der Länge $m$ . Eine Zielfunktion muss nun diese beiden Vektoren miteinander vergleichen, d.h. insbesondere ein Maß festlegen, mit dem die Abweichung oder der Fehler quantifiziert werden kann. Eine naheliegende Möglichkeit dafür ist nun die Euklidische Norm, die unserem gewohnten Abstandsbegriff in der (Euklidischen) Geometrie entspricht. Aus numerischen Gründen und aus Gründen der Einfachheit quadrieren wir dies noch, um die Wurzel, die sich innerhalb der Norm verbirgt, loszuwerden. Wir erhalten also die

Zielfunktion: $f(c) := \|Xc-y\|^2$

Diese Zielfunktion misst nun den quadratischen Approximations- oder Vorhersagefehler, auch Residuum genannt. Unser zu lösendes Problem hat also die Form

Optimierungsproblem der Linearen Regression: $\min_c f(c)$

In der Implementierung haben wir noch einen zusätzlichen Skalierungsfaktor $1/(2m)$ verwendet, der effektiv keinen Einfluß auf die Lösung hat, aber mathematisch/numerisch sinnvoll ist, letzen Endes ein Implementierungsdetail.

Visualisierung der Linearen Regression

Werfen wir nun noch einen genaueren Blick auf die Zielfunktion, um zu verstehen, was genau eigentlich optimiert wird. Die Zielfunktion lässt sich darstellen als

Zielfunktion: $f(c)=\|Xc - y\|^2 = \sum_j \left( c^Tx^{(j)}-y_j \right)^2$ ,

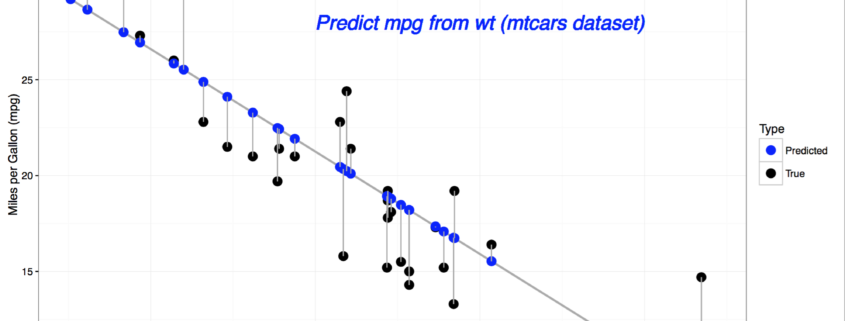
d.h. wir summieren die quadratischen Fehler pro Datenpunkt auf, was im nachfolgenden Plot veranschaulicht wird. Der punktweise (quadratische) Fehler ist die (quadrierte) Länge der grau eingezeichneten vertikalen Linien zwischen den echten $y$ -Werten (schwarz) und den approximierten oder durch die Lineare Regression vorhergesagten Werten $Xc$ (blau). Dieses Beispiel verwendet den in R “eingebauten” mtcars-Datensatz und stellt den Zusammenhang zwischen Gewicht (weigth, wt) und Reichweite pro Einheit Benzin (Miles per Gallon, mpg) dar.

Visualisierung der Linearen Regression

Die Zielfunktion ist also ein Polynom zweiten Grades in den Variablen $c_0,c_1,…,c_n$ . Es gibt daher strukturelle Ähnlichkeiten zu einigen der im zweiten Teil vorgestellten Testfunktionen, aber nun wollen wir uns dem eigentlichen Benchmark zuwenden.

Das algorithmische Setup

Um die in den ersten Teilen eingeführten verschiedenen Möglichkeiten der Schrittweitensteuerung für den Anwendungsfall der Linearen Regression zu benchmarken und testen, werden wir künstliche Daten nach einem bestimmten Schema erzeugen, um die verschiedenen Einflussgrößen geeignet zu parametrisieren. Konkret bedeutet dies, dass wir eine kleine Hilfskonstruktion verwenden, um ein Gleichungssystem zu erzeugen, bei dem wir bereits eine “einigermaßen gute” Lösung aufgrund der Konstruktionsvorschrift kennen. Dazu definieren wir einen

Hilfsvektor: $\hat{c}=[1,2,3,…,n+1].$

Dieser dient uns später als bereits bekannte, einigermaßen gute Näherungslösung. Weiter benötigen wir die oben angesprochene Matrix $X$ , außerdem einen

Fehlerterm: $z$ Vektor mit zufällig erzeugten Einträgen, gleichverteilt in $[0,1]$ , und normiert auf Länge $1$ .

Um diesen zufälligen, aber auf Einheitslänge normierten Fehler variieren zu können, definieren wir noch einen Skalierungsfaktor oder

Fehlergewicht: $\varepsilon$

Nun fehlt nur noch unsere abhängige Variable, der

Zielvektor: $y := X\hat{c} + \varepsilon z$ .

Diese Komnstruktion mag unnötig kompliziert aussehen, wir wissen nun aber aufgrund der obigen Vorschrift, dass innerhalb unseres Optimierungsproblems der Zielfunktionswert für den Hilfsvektor $\hat{c}$ folgendermaßen aussieht:

Funktionswert der Näherungslösung: $f(\hat{c}) := \|X\hat{c} -y\|^2 = \|X\hat{c}- X\hat{c} - \varepsilon z\|^2 = \varepsilon^2$ ,

da der Fehlerterm $z$ ja auf Einheitslänge normiert war. Dadurch kennen wir bereits vor Start unseres Algorithmus’ eine Näherungslösung und den zugehörigen Funktionswert. Dieser dient uns als triviale obere Schranke, so dass wir dann die Qualität der vom Verfahren gefundenen Lösung $c^*$ durch Vergleich mit der Näherungslösung $\hat{c}$ beurteilen können. Je kleiner $\varepsilon$ gewählt wird, umso näher sollten $c^*$ und $\hat{c}$ beisammen liegen.
Darüberhinaus ist solch ein Ansatz nicht unrealistisch, da in “echten” Problemstellungen die gesuchte Lösung zumeist ebenfalls von einem unbekannten Fehlerterm überlagert ist. Durch die hier gewählte Parametrisierung können wir direkt messen, welcher Anteil vom Fehlerterm letzten Endes in der Lösung präsent ist. Auch wenn dies in diesem Artikel nicht im Fokus des Interesses stehen wird, so kann ein solches Vorgehen unser Verständnis der Linearen Regression vertiefen helfen.
Wir fassen nun die wichtigsten Parameter des Optimierungsproblems der Linearen Regression noch einmal zusammen.

Die Anzahl der Datenpunkte: $m$ .
Die Anzahl der Parameter des linearen Modells: $n+1$ .
Die maximale Größe des Modellfehlers: $\varepsilon$ .

Eine kurze Anmerkung noch zur Anzahl $n+1$ der Modellparameter:
Eigentlich sind nur $n$ “echte” Variablen $x_1,…,x_n$ gegeben, so dass unser Problem die Dimension $n$ hat, man spricht dementsprechend auch von Linearer Regression in $n$ Dimensionen. Trotzdem besitzt das Modell $n+1$ Parameter. Dieser scheinbare Widerspruch lässt sich auflösen, wenn wir betrachten, welches Modell wir mit dem linearen Ansatz eigentlich an die Daten anpassen wollen. Zusammen mit den $y$ -Werten liegen unsere Daten nämlich in einem $n+1$ -dimensionalen Raum, und in genau diesem Raum wollen wir einen affin-linearen Zusammenhang bestimmen. In obigem Beispiel suchen wir eine Ausgleichgerade in dem durch $wt$ und $mpg$ aufgespannten zweidimensionalen Raum, und eine Gerade wird in zwei Dimensionen nun einmal durch zwei Parameter parametrisiert.
Mathematisch allgemein formuliert suchen wir einen linearen Unterraum der Dimension $n$ , der um eine Konstante verschoben ist, daher der Zusatz “affin”. Diese Konstante ist der zusätzliche Modellparameter, hier repräsentiert durch $c_0$ bzw. die Pseudovariable $x_0$ . Ohne den Zusatz “affin”, d.h. ohne die zusätzliche Verschiebung, würde jedes rein lineare Modell durch den Nullpunkt laufen müssen, was die Möglichkeiten der Anpassung an die Daten erheblich einschränken würde.

Ein erster Benchmark

Wir vergleichen im Folgenden die Performance des Gradientenverfahrens mit der Standard-Armijo-Regel, der Armijo-Regel mit Widening und einer exakten Schrittweite für verschiedene Wahlen der Parameter $m$ und $n+1$ . Das Fehlergewicht $\varepsilon$ spielt für die hier betrachteten Laufzeiten keine große Rolle, es ist eher hilfreich für ein qualitatives Verständnis der Linearen Regression, daher haben wir hier für alle Tests den Wert $\varepsilon=0.5$ gewählt. Das Verfahren bricht ab, wenn die Norm des Gradienten kleiner ist als $1e-6$ oder die Anzahl der Iteration gleich $100.000$ ist. Als Startpunkt wählen wir immer $c=[0,…,0]$ . Doch nun zu den eigentlichen Tests:

Lineare Regression in einer Dimension

In diesem Test wollen wir untersuchen, wie sich die verschiedenen Verfahren verhalten, wenn wir die Anzahl der Datenpunkte skalieren. Dafür betrachten wir das einfachste Problem, nämlich die Lineare Regression in einer Variablen, d.h. $n=1$ , aber Achtung, für die Anzahl der Modellparameter gilt allerdings $n+1=2$ wie oben erwähnt.

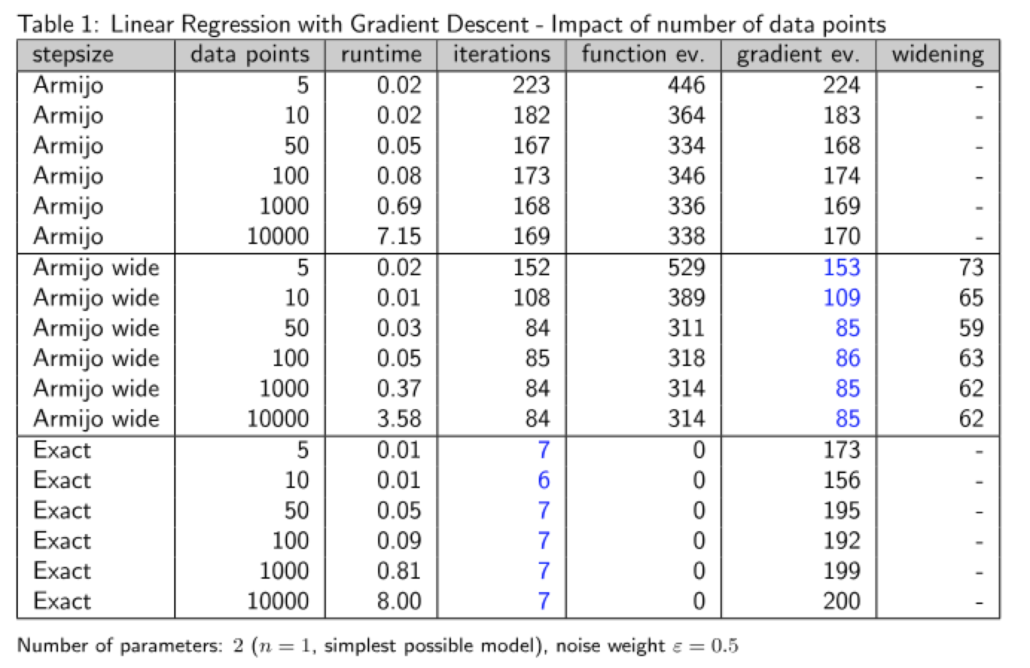
Verhalten der Verfahren bei wachsender Anzahl der Datenpunkte

Wie wir sehen, bleibt die Anzahl der Iterationen bei wachsender Anzahl an Datenpunkten in etwa gleich. Ein wenig überraschen mag vielleicht das gute Abschneiden der exakten Schrittweite, die in sehr wenigen Schritten konvergiert, ein Hinweis darauf, dass die Suchrichtung hier sehr gut ist, da sich das exakte Minimieren entlang dieser Richtung tatsächlich qualitativ in der Anzahl der benötigten Schritte erheblich bemerkbar macht. Von der Laufzeiten und der Anzahl der Gradientenauswertungen her ist die Armijo-Schrittweite mit Widening jedoch besser.

Lineare Regression in höheren Dimensionen

Was passiert aber, wenn wir die Anzahl der Dimensionen erhöhen? Dies ist Gegenstand unseres zweiten Tests, jetzt wollen wir für eine feste Anzahl an Datenpunkten: $m=1.000$ das Verhalten unserer Methoden “in echt” prüfen.

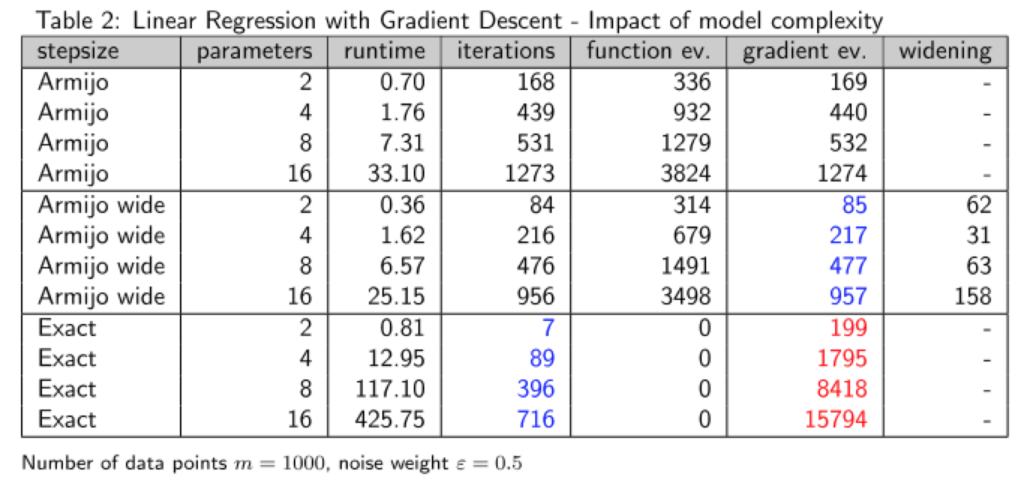
Verhalten der Verfahren bei wachsender Anzahl der Modellparameter

Wiederum ist die exakte Schrittweite gemessen an der Anzahl der Iterationen das beste Verfahren, allerdings fällt dieser Vorteil hier wesentlich geringer aus. Sowohl was die Laufzeiten angeht als auch die Anzahl der Gradientenauswertungen, ist die Armijo-Regel mit Widening klarer Gewinner.
Wir sehen hier allerdings zwei Effekte, die mit der Erhöhung der Variablen bzw. Modellparameter einhergehen. Zum einen erhöht sich die Anzahl der Iterationen, zum anderen erhöht sich wie im ersten Beispiel auch der Zeitaufwand pro Iterationsschritt. Solch ein Verhalten ist in der Praxis zu berücksichtigen, wenn man für eine gegebene Problemstellung ein passendes Modell sucht, insbesondere wenn man hohe Anforderungen in Bezug auf die Skalierbarkeit der Verfahren zu erfüllen hat.

Die hier betrachtete Performance der drei Verfahren im Vergleich entspricht ungefähr dem Average Case gemäß meiner Erfahrungen. Man kann auch Konstellationen finden, bei denen es keine Widening-Schritte gibt, so dass die Armijo-Regel mit Widening effektiv zur Armijo-Regel wird, ebenso lassen sich Szenarien angeben, bei denen der Widening-Effekt sogar zu einer geringeren Anzahl an Schritten führt als die exakte Schrittweite. Dem Grundsatz nach kann man anhand dieser Beispiele jedoch ablesen, dass zum einen die inexakten Schrittweiten im Falle des Gradientenverfahrens tatsächlich performanter sind, und dass zum anderen die minimale Erweiterung der Armijo-Regel mit Widening bereits Performance-Gewinne in Höhe von ca. 20-25% ermöglicht.

Ein kurzer Ausflug in die Welt der festen Schrittweiten

Um mal einen ganz konkreten Anhaltspunkt zu geben, warum man feste Schrittweiten in quasi allen Fällen vermeiden sollte, wollen wir den letzten Test noch einmal mit verschiedenen Werten einer festen Schrittweite wiederholen. Wir erinnern uns: Theoretisch funktioniert das Gradientenverfahren auch mit einer vom konkreten Problem abhängigen, möglicherweise sehr kleinen, aber festen Schrittweite, so dass eine Schrittweitensteuerung überflüssig sein könnte. Hier nun die Realität hinter der Theorie:

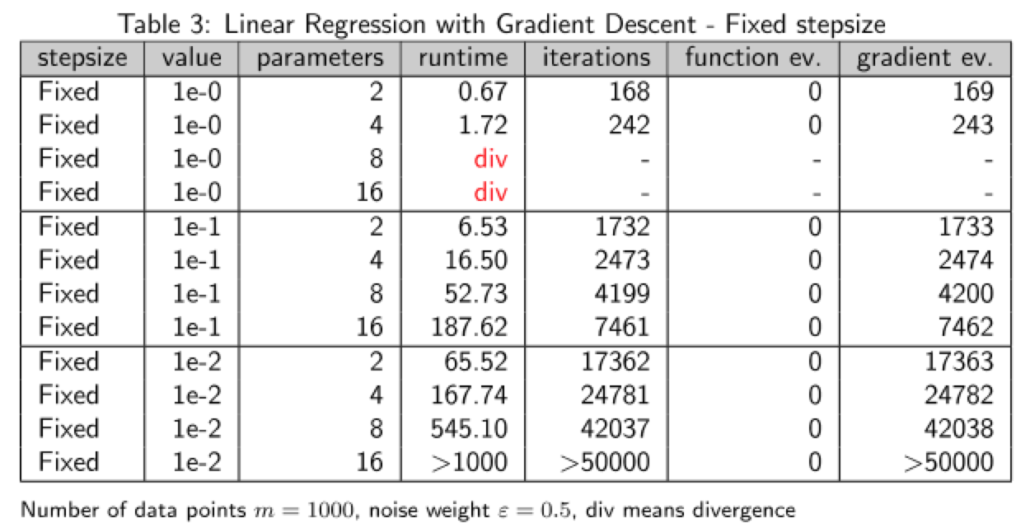
Verhalten des Gradientenverfahrens mit fester Schrittweite

Die feste Schrittweite ist nur im Falle des einfachsten Problems überhaupt einigermaßen konkurrenzfähig, außerdem muss man dafür auch noch eine extrem große Schrittweite wählen – im Fall $1e-0$ bedeutet es ja, dass immer ein voller Gradientenschritt ausgeführt wird. Im allgemeinen sind solche großen Schrittweiten viel zu riskant, was man auch an der Divergenz – markiert durch das rote div – im Fall komplexerer Modelle sieht. Und in Teil 2 dieser Serie hatten wir ja gesehen, dass man für kompliziertere Zielfunktionen wie die Rosenbrock-Funktion teilweise Werte von $1e-7$ verwenden muss, damit das Verfahren konvergiert. Eine solche Wahl würde die Laufzeit im Fall der Linearen Regression vollends explodieren lassen.

Zusammenfassung

Insgesamt hat also die Armijo-Regel mit Widening den besten Eindruck hinterlassen, auch wenn die exakte Schrittweite mit einer grundsätzlich geringeren Anzahl an Iterationen punkten konnte. Diese beiden Ergebnisse weisen aber beide in dieselbe Richtung, denn sie bedeuten, dass die Suchrichtung des Gradientenverfahrens – der negative Gradient – für die Lineare Regression grundsätzliche keine schlechte Wahl ist. Bei der Widening-Idee liegt dieser Schluss nahe, da ja größere Schritte in eine Richtung einen stärkeren Abstieg implizieren – je länger man in eine Ricntung gehen kann und die Zielfunktion abnimmt, umso besser.
Aber auch die qualitative Stärke der exakten Schrittweite bedeutet im Wesentlichen dasselbe. Wenn es sich nämlich lohnt, die Zielfunktion in einer bestimmten Suchrichtung – mit welchem Aufwand auch immer – zu minimieren, und im Ergebnis werden weniger Schritte benötigt, so muss diese “lokale” oder eindimensionale Optimierung entlang einer Richtung qualitativ sinnvoll gewesen sein im Hinblick auf das “globale” oder mehrdimensionale Problem, welches ja eigentlich gelöst werden soll.
In beiden Fällen ist also die Implikation, dass die lokale Suchrichtung nicht allzu weit von der global optimalen Richtung – diejenige Richtung, die direkt zur Lösung zeigt – abweichen kann. Wir hatten in Teil 2 ja bereits die Suchrichtung des negativen Gradienten mit dieser optimalen Richtung anhand von Beispielen verglichen.

Im Fall der Linearen Regression lohnt es sich also tatsächlich, sich die verschiedenen Möglichkeiten, die die Toolbox der Unrestringierten Optimierung zur Verfügung stellt, einmal näher anzuschauen. Ob und inwiefern das auch für andere Verfahren des Maschinellen Lernens gilt, werden wir in den nächsten Artikeln beleuchten. Weiter geht es dann mit dem Prototyp eines Klassifikationsverfahrens, der Logistischen Regression.

Dr. Stefan Kühn

Dr. Stefan Kühn ist promovierter Mathematiker mit Schwerpunkten in Optimierung und Numerischer Mathematik. Er arbeitet als Senior Data Scientist bei XING Marketing Solutions und entwickelt dort u.a. Machine-Learning-Modelle für die komplexen Fragestellungen im Big-Data-Umfeld. Vor seiner Zeit bei XING war Stefan bei Zalando und der codecentric AG tätig.