Wie lernen Maschinen?

Machine Learning ist eines der am häufigsten verwendeten Buzzwords im Data-Science- und Big-Data-Bereich. Aber lernen Maschinen eigentlich und wenn ja, wie? In den meisten Fällen lautet die Antwort: Maschinen lernen nicht, sie optimieren. Fällt der Begriff Machine Learning oder Maschinelles Lernen, so denken viele sicherlich zuerst an bekannte “Lern”-Algorithmen wie Lineare Regression, Logistische Regression, Neuronale Netze oder Support Vector Machines. Die meisten dieser Algorithmen – wir beschränken uns hier vorerst auf den Bereich des Supervised Learning – sind aber nur Anwendungen einer anderen, grundlegenderen Theorie – der mathematischen Optimierung. Alle hier angesprochenen Algorithmen stellen dem Anwender eine bestimmte Ziel- oder Kostenfunktion zur Verfügung, aus der sich i.a. der Name der Methode ableitet und für die im Rahmen des Lernens ein Minimum oder Optimum gefunden werden soll. Ein großer Teil des Geheimnisses und die eigentliche Stärke der Machine-Learning-Algorithmen liegt nun darin, dass dieser Minimierungsprozess effizient durchgeführt werden kann. Wir wollen im Folgenden kurz erklären, wie dies in etwa funktioniert. In einem späteren Blogpost gehen wir dann genauer auf das Thema der Effizienz eingehen.

Unrestringierte Optimierung

Innerhalb der Optimierungstheorie unterscheidet man zwischen Problemstellungen mit Nebenbedingungen, etwa wenn bestimmte Variablen nicht negativ sein dürfen, und solchen ohne Nebenbedingungen, und genau diese angenehme Situation liegt bei den meisten Anwendungen des Machine Learning vor. Das Ziel dieser sog. unrestringierten Optimierung ist die Minimierung einer gegebenen Zielfunktion $f$ , gern auch Kostenfunktion genannt, da die Werte dieser Funktion in der praktischen Anwendung meist mit bestimmten Kosten assoziiert sind. Allgemein beschreibt die Zielfunktion im Rahmen des Machine Learning die Abweichung des gewählten Modells von den vorliegenden Daten. Im Fall der linearen Regression in einer Variablen wird beispielsweise der Fehler eines linearen Modells, d.h. einer Ausgleichsgerade durch alle Datenpunkte gemessen. Aufgabe der Optimierungsverfahren ist es, diesen Fehler zu minimieren. Dazu gehen die meisten Methoden iterativ vor.

Ein prototypischer Minimierungsalgorithmus

Initialisierung:

Wähle einen Startpunkt.

Iteration:

Teste ein Abbruchkriterium: Ist der aktuelle Punkt nah genug am Minimum?
Finde eine Abstiegsrichtung: Werden die Funktionswerte in dieser Richtung zumindest in der Nähe des aktuellen Punktes kleiner?
Bestimme eine passende Schrittweite: Wie lang soll/darf/kann der Schritt in die gefundene Abstiegsrichtung sein, so dass genug Abstieg der Zielfunktion erzielt wird?

Aus diesen Komponenten setzen sich die allermeisten iterativen Optimierungsverfahren zusammen. Die angegebene Reihenfolge der Arbeitsschritte dieses Meta-Algorithmus’ entspricht einem Line-Search-Verfahren (Liniensuche). Vertauscht man die letzten beiden Punkte und bestimmt zuerst eine Schrittweite und danach eine Suchrichtung, so erhält man ein Trust-Region-Verfahren (Vertrauensbereich). Im Folgenden wollen wir die drei Aufgaben innerhalb der Iteration näher kennenlernen, wir beschränken uns dabei auf Funktionen, die mindestens einmal stetig differenzierbar sind, was für unsere Zwecke eigentlich keine Einschränkung ist, da die allermeisten Supervised-Learning-Verfahren dieser Anforderung genügen. Wichtig ist, dass wir die erste Ableitung bestimmen können, die ja bekanntlich Informationen über die Steigung einer Funktion enthält.

Ein einfaches Abbruchkriterium

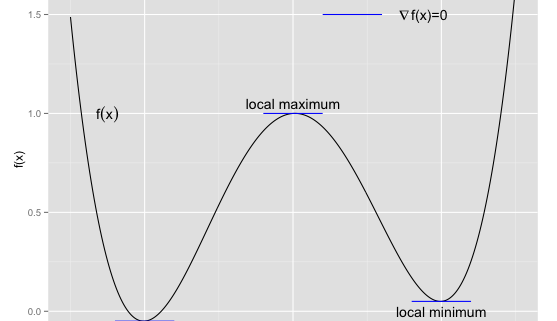
Die erste Ableitung oder besser der Gradient einer Funktion $f(x)$ wird mit $\nabla f(x)$ oder einfach $\nabla f$ bezeichnet. Die folgende Grafik veranschaulicht eine wichtige Bedeutung, die der Gradient innerhalb der Optimierungstheorie besitzt.

Man kann unschwer erkennen, dass die wichtigen Stellen des Graphen einer Funktion eine Gemeinsamkeit haben, der Gradient verschwindet:

$\nabla f(x)=0$ .

Maxima stören uns nicht, denn der Algorithmus wird immer nur Schritte in eine Abstiegsrichtung unternehmen. Es könnte höchstens sein, dass unser Startpunkt bereits ein Maximum ist, dann können wir auf einfache Art und Weise keine Abstiegsrichtung ermitteln oder testen, wie wir noch sehen werden. In diesem pathologischen Fall – die Wahrscheinlichkeit dafür bewegt sich normalerweise nahe bei Null – sollte man ohnehin einen neuen Startpunkt wählen, da man sonst nicht zwischen Minimum und Maximum unterscheiden kann. Allerdings ist es nicht immer so einfach, wie es hier aussieht, es gibt auch komplexere Funktionen, die sog. Wendestellen besitzen, doch in den meisten Machine-Learning-Anwendungen sind solche Situationen ausgeschlossen. Für jetzt halten wir fest:

Abbruchkriterium: Der Algorithmus wird erfolgreich beendet, wenn $\|\nabla f(x)\| < \varepsilon$ für eine vorgegebene Toleranz $\varepsilon > 0$ .

Nachdem wir nun zuallererst geklärt haben, wie das Ende eines Algorithmus-Durchlaufes aussieht, kommen wir zu den zentralen Elementen.

Abstiegsrichtungen

Intuitiv ist eine Abstiegsrichtung eine Richtung, in der die Funktionswerte kleiner werden, wenn wir uns “ein kleines Stück” bewegen. Bevor wir dieses Konzept formalisieren, wollen wir uns mit der Geometrie hinter dieser Intuition vertraut machen.

In dieser Grafik – es handelt sich um einen sog. Contour-Plot – sind die Höhenlinien einer einachen Funktion zu sehen, in diesem Fall handelt es sich um Kreise, und entlang dieser Kreislinien ist die Funktion konstant. Das Minimum dieser Funktion befindet sich im Zentrum der Kreise, die Funktionswerte nehmen also nach außen hin zu. Die grüne Tangente an die Höhenlinien teilt die abgebildete Ebene in zwei Hälften. Alle Richtungen, die wie der schwarz eingezeichnete Gradient $\nabla f$ nach außen zeigen, können keine Abstiegsrichtungen sein, da nach außen hin die Funktionswerte wachsen. Nur die Richtungen nach innen sind demnach Abstiegsrichtungen. Die Grenze zwischen Abstiegsrichtungen und allen anderen Richtungen wird also durch die grüne Tangente definiert, und diese bildet immer einen rechten Winkel mit dem Gradienten.

Ein einfacher Test

Mathematisch kann der Winkel zwischen zwei Vektoren durch das Skalarprodukt dieser Vektoren berechnet werden. Zwei Vektoren schließen einen Winkel von 90° ein, d.h. sie sind orthogonal zueinander, wenn das Skalarprodukt beider Vektoren Null ist. Diese Bedingung entspricht also unserer grün eingezeichneten Linie. Für alle Vektoren, die nach innen zeigen, ist das Skalarprodukt kleiner Null. Wir müssen also den genauen Winkel gar nicht bestimmen, es reicht aus, das Vorzeichen des Skalarproduktes einer Suchrichtung mit dem Gradienten zu betrachten. Die Bedingung an eine Abstiegsrichtung ist also

Abstiegsrichtung: $\langle d,\nabla f \rangle = d^T\nabla f < 0.$

Wir haben jetzt einen einfachen Test, aber noch keine konkrete Abstiegsrichtung gesehen. Eine offensichtliche Wahl sei hier aber bereits verraten, der negative Gradient $-\nabla f$ . Da dieser immer in die entgegengesetzte Richtung zeigt, ist die Bedingung trivialerweise immer erfüllt. Diese Abstiegsrichtung hat übrigens dem Gradientenverfahren, auch Verfahren des steilsten Abstiegs oder Gradient Descent, seinen Namen gegeben.

Die Schrittweite

Es gibt eine Vielzahl von Verfahren zur Bestimmung einer Schrittweite, die einfachste und wahrscheinlich bekannteste Methode ist die sog. Armijo-Regel. Wir kommen diesmal gleich zu den technischen Details und motivieren diese später. Die Armijo-Regel benötigt eine Abstiegsrichtung $d$ und zwei Parameter, $0< \sigma < 1$ , und $0 < \rho < 0.5$ . Nun suchen wir in der Folge $\ell = 0,1,2,…$ das erste $\ell$ , welches die Armijo-Bedingung erfüllt:

Schrittweite: $f(x+\sigma^{\ell} d) < f(x) +\rho \sigma^{\ell}\nabla f(p)^Td.$

Bevor wir uns durch diese kompliziert aussehende Formel arbeiten, hier eine kleine graphische Unterstützung:

Betrachten wir noch einmal beide Seiten der Armijo-Bedingung. Auf der linken Seite steht die Funktion, wie sie entlang der gewählten Abstiegsrichtung $d$ weitergeht. Auf der rechten Seite steht die durch den Parameter $\rho$ und die Schrittweite $t$ definierte rote Gerade. Aufgrund der Wahl von $\rho < 0.5$ muss die Funktion zumindest ein kleines Stück unterhalb der roten Gerade verlaufen, denn zu Beginn verläuft sie entlang der grünen Linie, die der Wahl von $\rho =1$ entspricht. Es muss also kleine Werte von $t$ , insgesamt sogar ein ganzes Interval geben, so dass die Armijo-Bedingung erfüllt ist. Die obige Vorschrift startet nun mit $t=1$ – das entspricht $\ell=0$ – und testet die Armijo-Bedingung und halbiert nötigenfalls die Schrittweite so lange, bis die Armijo-Bedingung erfüllt ist.

Zusammenfassung

Wir wissen nun, wie ein allgemeines Lern- oder Optimierungsverfahren funktioniert, wir haben alle benötigten Zutaten beisammen. Damit Maschinen lernen können, benötigen sie also recht präzise Vorgaben, und in einem weiteren Artikel werden wir nach der ganzen Theorie diese Einzelteile in Aktion erleben. Außerdem wollen wir uns dann damit beschäftigen, wie mit kleinen Veränderungen große Verbesserungen erreicht werden können in Bezug auf die Lerngeschwindigkeit. Es lohnt sich also durchaus, diesem Aspekt des Maschinellen Lernens einmal ein wenig Aufmerksamkeit zu schenken.

Nachfolgender Artikel – Wie lernen Maschinen? Teil 2

Dr. Stefan Kühn

Dr. Stefan Kühn ist promovierter Mathematiker mit Schwerpunkten in Optimierung und Numerischer Mathematik. Er arbeitet als Senior Data Scientist bei XING Marketing Solutions und entwickelt dort u.a. Machine-Learning-Modelle für die komplexen Fragestellungen im Big-Data-Umfeld. Vor seiner Zeit bei XING war Stefan bei Zalando und der codecentric AG tätig.