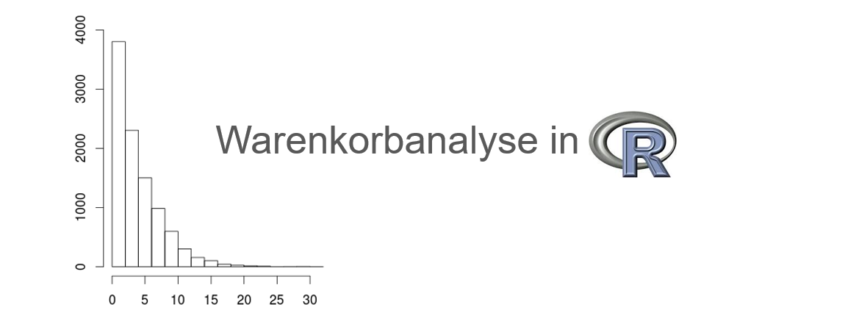Was ist die Warenkorbanalyse?
Die Warenkorbanalyse ist eine Sammlung von Methoden, die die beim Einkauf gemeinsam gekauften Produkte oder Produktkategorien aus einem Handelssortiment untersucht. Ziel der explorativen Warenkorbanalyse ist es, Strukturen in den Daten zu finden, so genannte Regeln, die beschreiben, welche Produkte oder Produktkategorien gemeinsam oder eben nicht gemeinsam gekauft werden.
Beispiel: Wenn ein Kunde Windeln und Bier kauft, kauft er auch Chips.
Werden solche Regeln gefunden, kann das Ergebnis beispielsweise für Verbundplatzierungen im Verkaufsraum oder in der Werbung verwendet werden.
Datenaufbau
Die Daten, die für diese Analyse untersucht werden, sind Transaktionsdaten des Einzelhandels. Meist sind diese sehr umfangreich und formal folgendermaßen aufgebaut:

Ausschnitt eines Beispieldatensatzes: Jede Transaktion (= Warenkorb = Einkauf) hat mehrere Zeilen, die mit der selben Transaktionsnummer (Spalte Transaction) gekennzeichnet sind. In den einzelnen Zeilen der Transaktion stehen dann alle Produkte, die sich in dem Warenkorb befanden. In dem Beispiel sind zudem noch zwei Ebenen von Produktkategorien als zusätzliche Informationen enthalten.
Es gibt mindestens 2 Spalten: Spalte 1 enthält die Transaktionsnummer (oder die Nummer des Kassenbons, im Beispielbild Spalte Transaction), Spalte 2 enthält den Produktnamen. Zusätzlich kann es weitere Spalten mit Infos wie Produktkategorie, eventuell in verschiedenen Ebenen, Preis usw. geben. Sind Kundeninformationen vorhanden, z.B. über Kundenkarten, so können auch diese Informationen enthalten sein und mit ausgewertet werden.
Beschreibende Datenanalyse
Die Daten werden zunächst deskriptiv, also beschreibend, analysiert. Dazu werden z.B. die Anzahl der Transaktionen und die Anzahl der Produkte im Datensatz berechnet. Zudem wird die Länge der Transaktionen, also die Anzahl der Produkte in den einzelnen Transaktionen untersucht. Dies wird mit deskriptiven Maßzahlen wie Minimum, Maximum, Median und Mittelwert in Zahlen berichtet sowie als Histogramm grafisch dargestellt, siehe folgende Abbildung.

Histogramm der Längenverteilung der Transaktionen.
Die häufigsten Produkte werden ermittelt und können gesondert betrachtet werden. Als Visualisierung kann hier ein Balkendiagramm mit den relativen Häufigkeiten der häufigsten Produkte verwendet werden, wie im folgenden Beispiel.

Relative Häufigkeiten der häufigsten Produkte, hier nach relativer Häufigkeit größer 0,1 gefiltert.
Ähnliche Analysen können bei Bedarf auch auf Kategorien-Ebene oder nach weiteren erhobenen Merkmalen selektiert durchgeführt werden, je nachdem, welche Informationen in den Daten stecken und welche Fragestellungen für den Anwender interessant sind.
Verbundanalyse
Im nächsten Schritt wird mit statistischen Methoden nach Strukturen in den Daten gesucht, auch Verbundanalyse genannt. Als Grundlage werden Ähnlichkeitsmatrizen erstellt, die für jedes Produktpaar die Häufigkeit des gemeinsamen Vorkommens in Transaktionen bestimmen. Solch eine Ähnlichkeitsmatrix ist zum Beispiel eine Kreuztabelle in der es für jedes Produkt eine Spalte und eine Zeile gobt. In den Zellen in der Tabelle steht jeweils die Häufigkeit, wie oft dieses Produktpaar gemeinsam in Transaktionen in den Daten vorkommt, siehe auch folgendes Beispiel.

Ähnlichkeitsmatrix oder Kreuztabelle der Produkte: Frankfurter und Zitrusfrüchte werden in 64 Transaktionen zusammen gekauft, Frankfurter und Berries in 22 usw.
Auf Basis solch einer Ähnlichkeitsmatrix wird dann z.B. mit Mehrdimensionaler Skalierung oder hierarchischen Clusteranalysen nach Strukturen in den Daten gesucht und Gemeinsamkeiten und Gruppierungen gefunden. Die hierarchische Clusteranalyse liefert dann ein Dendrogram, siehe folgende Abbildung, in der ähnliche Produkte miteinander gruppiert werden.

Dendrogram als Visualisierung des Ergebnisses der hierarchischen Clusterananlyse. Ähnliche Produkte (also Produkte, die zusammen gekauft werden) werden zusammen in Gruppen geclustert. Je länger die vertikale Verbindungslinie ist, die zwei Gruppen oder Produkte zusammen fasst, um so unterschiedlicher sind diese Produkte bzw. Gruppen.
Assoziationsregeln
Schließlich sollen neben den Verbundanalysen am Ende in den Daten Assoziationsregeln gefunden werden. Es werden also Regeln gesucht und an den Daten geprüft, die das Kaufverhalten der Kunden beschreiben. Solch eine Regel ist zum Beispiel „Wenn ein Kunde Windeln und Bier kauft, kauft er auch Chips.“ Formal: {Windeln, Bier} → {Chips}
Für diese Regeln lassen sich statistische Maßzahlen berechnen, die die Güte und Bedeutung der Regeln beschreiben. Die wichtigsten Maßzahlen sind Support, Confidence und Lift:
Support ist das Signifikanzmaß der Regel. Es gibt an, wie oft die gefundene Regel in den Daten anzuwenden ist. Wie oft also die in der Regel enthaltenen Produkte gemeinsam in einer Transaktion vorkommen. In dem Beispiel oben: Wie oft kommen Windeln, Bier und Chips in einer Transaktion gemeinsam vor?
Confidence ist das Qualitätsmaß der Regel. Es beschreibt, wie oft die Regel richtig ist. In dem oben genanten Beispiel: Wie oft ist in einer Transaktion Chips enthalten, wenn auch Windeln und Bier enthalten sind?
Lift ist das Maß der Bedeutung der Regel. Es sagt aus wie oft die Confidence den Erwartungswert übersteigt. Wie ist die Häufigkeit des gemeinsamen Vorkommens von Windeln, Bier und Chips im Verhältlnis zur erwarteten Häufigkeit des Vorkommens, wenn die Ereignisse stochastisch unabhängig sind?
Algorithmen
In den Daten werden zunächst alle möglichen Regeln gesammelt, die einen Mindestwert an Support und Confidence haben. Die Mindestwerte werden dabei vom Nutzer vorgegeben. Da es sich bei Transaktionsdaten um große Datenmengen handelt und häufig große Anzahlen von Produkten enthalten sind, wird die Suche nach Regeln zu einem komplexen Problem. Es wurden verschiedene effiziente Algorithmen als Suchstrategien entwickelt, z.B. der APRIORI-Algorithmus von Agrawal und Srikant (1994), der auch im weiter unten vorgestellten Paket arules von R verwendet wird.
Sind die Assoziationsregeln gefunden, können Sie vom Nutzer genauer untersucht werden und z.B. nach den oben genannten Kennzahlen sortiert betrachtet werden, oder es werden die Regeln für spezielle Warenkategorien genauer betrachtet, siehe folgendes Beispiel.

Beispielausgabe von Regeln, hier die drei Regeln mit dem besten Lift. In der ersten Regel sieht man: Wenn Bier und Wein gekauft wird, wird auch Likör gekauft. Diese Regel hat einen Support von 0,002. Diese drei Produkte kommen also in 0,2 % der Transaktionen vor. Die Confidence von 0,396 zeigt, dass in 39,6 % der Transaktionen auch Likör gekauft wird, wenn Bier und Wein gekauft wird.
Umsetzung mit R
Die hier vorgestellten Methoden zur Warenkorbanalyse lassen sich mit dem Paket arules der Software R gut umsetzen. Im Folgenden gebe ich eine Liste von nützlichen Befehlen für diese Analysen mit dieser Software. Dabei wird mit data hier durchgehend der Datensatz der Transaktionsdaten bezeichnet.
Zusammenfassung des Datensatzes:
- Anzahl der Transaktionen und Anzahl der Warengruppen
- die häufigsten Produkte werden genannt mit Angabe der Häufigkeiten
- Längenverteilung der Transaktionen (Anzahl der Produkte pro Transaktion): Häufigkeiten, deskriptive Maße wie Quartile
- Beispiel für die Datenstruktur (Levels)
Längen der Transaktionen (Anzahl der Produkte pro Transaktion)
Histogramm als grafische Darstellung der Transaktionslängen
|
|
itemFrequencyPlot(data, support=0.1) |
rel. Häufigkeiten der einzelnen Produkte, hier nur die mit mindestens 10 % Vorkommen
Äquivalenzmatrix: Häufigkeiten der gemeinsamen Käufe für Produktpaare
|
|
dissJacc <- dissimilarity(data[, itemFrequency(data) > 0.05], method = "Jaccard", which = "items") |
Unähnlichkeitsmatrix für die hierarchische Clusteranalyse
|
|
hcWard <- hclust(dissJacc, method = "ward.D") |
Hierarchische Clusteranalyse
Dendrogram der hierarchischen Clusteranalyse
|
|
rules <- apriori(data, parameter = list(support = 0.001, confidence = 0.2), control = list(verbose = FALSE)) |
Assoziationsregeln finden mit APRIORI-Algorithmus, hier Regeln mit mindestens 1% Support und 20 % Confidence
Zusammenfassung der oben gefundenen Regeln (Anzahl, Eigenschaften Support, Confidence, Lift)
|
|
inspect(SORT(rules,by=“lift“)[1:5]) |
Einzelne Regeln betrachten, hier die laut Lift besten 5 Regeln
Referenzen:
- Michael Hahsler, Kurt Hornik, Thomas Reutterer: Warenkorbanalyse mit Hilfe der Statistik-Software R, Innovationen in Marketing, S.144-163, 2006.
- Michael Hahsler, Bettina Grün, Kurt Hornik, Christian Buchta, Introduciton to arules – A computational environment for mining association rules and frequent item sets. (Link zum PDF)
- Rakesh Agrawal, Ramakrishnan Srikant, Fast algorithms for mining association rules, Proceedings of the 20th VLDB Conference Santiago, Chile, 1994
- Software R: R Core Team (2016). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Link: R-Project.org.
- Paket: arules: Mining Association Rules using R.
Beispieldatensatz: Groceries aus dem Paket arules