Octave – Data Science Blog

Im letzten Artikel der Serie haben wir gesehen wie bereits trainierte Netzwerke verwendet werden können. Als Training wird der Prozess bezeichnet der die Gewichte in einen Netzwerk so anpasst, dass bei einem Vorwärtspass durch ein Netzwerk zu einen festgelegten Eingangsdatensatz ein bestimmtes Ergebnis in der Ausgangsschicht ausgegeben wird. Im Umkehrschluss heißt das auch, dass wenn etwas anderes ausgeliefert wurde als erwartet, das Netzwerk entweder noch nicht gut genug oder aber auf ein anderes Problem hin trainiert wurde.

Training

Das Training selbst findet in drei Schritten statt. Zunächst werden die Gewichte initialisiert. Üblicherweise geschieht das mit zufälligen Werten, die aus einer Normalverteilung gezogen werden. Je nachdem wie viele Gewichte eine Schicht hat, ist es sinnvoll die Verteilung über den Sigma Term zu skalieren. Als Daumenregeln kann dabei eins durch die Anzahl der Gewichte in einer Schicht verwendet werden.

Im zweiten Schritt wird der Vorwärtspass für die Trainingsdaten errechnet. Das Ergebnis wird beim ersten Durchlauf alles andere als zufrieden stellend sein, es dient aber dem Rückwärtspass als Basis für dessen Berechnungen und Gewichtsänderungen. Außerdem kann der Fehler zwischen der aktuellen Vorhersage und dem gewünschten Ergebnis ermittelt werden, um zu entscheiden, ob weiter trainiert werden soll.

Der eigentliche Rückwärtspass errechnet aus der Differenz der Vorwärtspassdaten und der Zieldaten die Steigung für jedes Gewicht aus, in dessen Richtung dieses geändert werden muss, damit das Netzwerk bessere Vorhersagen trifft. Das klingt zunächst recht abstrakt, die genauere Mathematik dahinter werde ich in einem eigenen Artikel erläutern. Zur besseren Vorstellung betrachten wir die folgende Abbildung.

visuelle Darstellung aller Gewichtskombinationen und deren Vorhersagefehler

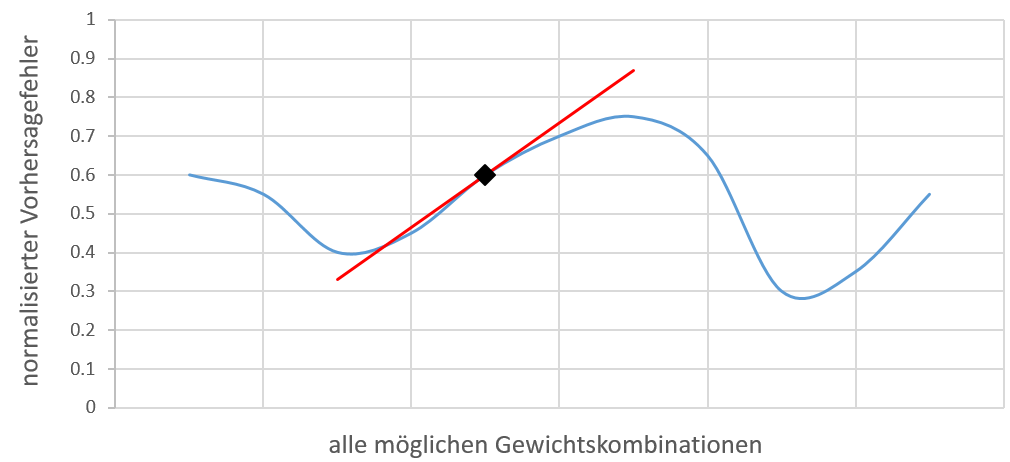
Das Diagramm zeigt in blau zu allen möglichen Gewichtskombinationen eines bestimmten, uns unbekannten, Netzwerks und Problems den entsprechenden Vorhersagefehler. Die Anzahl der Kombinationen hängt von der Anzahl der Gewichte und der Auflösung des Wertebereiches für diese ab. Theoretisch ist die Menge also unendlich, weshalb die blaue Kurve eine von mir ausgedachte Darstellung aller Kombinationen ist. Der erste Vorwärtspass liefert uns eine Vorhersage die eine normalisierte Differenz von 0.6 zu unserem eigentlichen Wunschergebnis aufweist. Visualisiert ist das Ganze mit einer schwarzen Raute. Der Rückwärtspass berechnet aus der Differenz und den Daten vom Vorwärtspass einen Änderungswunsch für jedes Gewicht aus. Da die Änderungen unabhängig von den anderen Gewichten ermittelt wurden, ist nicht bekannt was passieren würde wenn alle Gewichte sich auf einmal ändern würden. Aus diesem Grund werden die Änderungswünsche mit einer Lernrate abgeschwächt. Im Endeffekt ändert sich jedes Gewicht ein wenig in die Richtung, die es für richtig erachtet. In der Hoffnung einer Steigerung entlang zu einem lokalen Minimum zu folgen, werden die letzten beiden Schritte (Vor- und Rückwärtspass) mehrfach wiederholt. In dem obigen Diagramm würde die schwarze Raute der roten Steigung folgen und sich bei jeder Iteration langsam auf das linke lokale Minimum hinzubewegen.

Anwendungsbeispiel und Programmcode

Um den ganzen Trainingsprozess im Einsatz zu sehen, verwenden wir das Beispiel aus dem Artikel “KNN: Vorwärtspass”. Die verwendeten Daten kommen aus der Wahrheitstabelle eines X-OR Logikgatters und werden in ein 2-schichtiges Feedforward Netzwerk gespeist.

XOR Wahrheitstabelle

X1	X2	Y = X1 ⊻ X2
0	0	0
0	1	1
1	0	1
1	1	0

Der Programmcode ist in Octave geschrieben und kann zu Testzwecken auf der Webseite von Tutorialpoint ausgeführt werden. Die erste Hälfte von dem Algorithmus kennen wir bereits, der Vollständigkeit halber poste ich ihn noch einmal, zusammen mit den Rückwärtspass. Hinzugekommen sind außerdem ein paar Konsolenausgaben, eine Lernrate- und eine Iterations-Variable die angibt wie viele Trainingswiederholungen durchlaufen werden sollen.

%--------------------- Daten -----------------------

X = [0 0; % Eingangsdaten

0 1;

1 0;

1 1]

Y = [0;1;1;0] % erwartete XOR Ausgangsdaten

theta1 = normrnd(0, 1/(3*2), 3, 2); % 3x2 Gewichtsmatrix

theta2 = normrnd(0, 1/(3*1), 3, 1); % 3x1 Gewichtsmatrix

m = length(X) % Anzahl der Eingangsdaten

iteration = 10000 % Anzahl der Trainingsiterationen

alpha = 0.8 % lernrate

printf("\n\nStarte Training ... ")

for(i = 1:iteration)

%--------------------- Vorwärtspass -----------------------

V = X; % anlegen der Eingangsdaten an die Eingangsschicht

% 1. berechne die Aktivierungen der verborgenen Schicht

Vb = [ones(m,1) V]; % hinzufügen der Bias Units (sind immer 1)

Zv = Vb * theta1; % Summe aus den Eingangswerten multipliziert mit deren Gewichten

H = 1 ./ (1 .+ e.^-Zv); % anwenden der Sigmoid Funktion auf die Aktivierungsstärke Zv

% 2. berechne die Aktivierungen der Ausgangsschicht

Hb = [ones(m,1) H]; % hinzufügen der Bias Units an die verborgene Schicht

Zh = Hb * theta2; % Produkt aus den Aktivierungen der Neuronen in H und Theta2

O = 1 ./ (1 .+ e.^-Zh); % Vorhersage von dem Netzwerk

% 3. berechne die Vorhersageungenauigkeit

loss = (O .- Y) .^ 2; % quadratischer Fehler von der Vorhersage und der Zielvorgabe Y

mse = sum(loss) / m; % durchschnittlicher quadratischer Fehler aller Vorhersagen

%--------------------- Rückwärtspass -----------------------

% 1. Ableitung der Fehlerfunktion

d = O .- Y; % Differenzmatrix zwischen der Vorhersage und der Zielvorgabe Y

% 2. berechne die Änderungen für Theta2 und die Ableitung der Ausgangsschicht

OMO = ones(size(O)) .- O; % Zwischenvariable: 1-Minus-Vorhersage

Zhd = d .* O .* OMO; % Ableitung der Sigmoid Funktion

theta2c = Hb' * Zhd; % Änderunswunsch für Theta2

Hd = Zhd * theta2'; % Ableitung von der Ausgangsschicht

Hd(:,[1]) = []; % Ableitung von der Bias Unit

% 3. berechne die Änderungen für Theta1 und die Ableitung der verborgenen Schicht

HMO = ones(size(H)) .- H; % Zweischenvariable: 1 Minus Aktivierung der verborgenen Schicht

Zvd = Hd .* H .* HMO; % Ableitung der Sigmoid Funktion von der Aktivierungsstärke Zv

theta1c = Vb' * Zvd; % Änderunswunsch für Theta1

% weitere Ableitungen sind nicht notwendig

theta1 -= theta1c .* alpha; % ändere die Gewichte von Theta1 und Theta2

theta2 -= theta2c .* alpha; % der Änderungswunsch wird von der Lernrate abgeschwächt

endfor

% Ausgabe von der letzten Vorhersage und den Gewichten

printf("abgeschlossen. \n")

printf("Letzte Vorhersage und trainierte Gewichte\n")

theta1

theta2

Zu jeder Zeile bzw. Funktion die wir im Vorwärtspass geschrieben haben, gibt es im Rückwärtspass eine abgeleitete Variante. Dank den Ableitungen können wir die Änderungswünsche der Gewichte in jeder Schicht ausrechnen und am Ende einer Trainingsiteration anwenden. Wir trainieren 10.000 Iterationen lang und verwenden eine Lernrate von 0,8. In komplexeren Fragestellungen, mit mehr Daten, würden diese Werte niedriger ausfallen.

Es ist außerdem möglich den ganzen Programmcode viel modularer aufzubauen. Dazu werde ich im nächsten Artikel auf eine mehr objekt-orientiertere Sprache wechseln. Nichts desto trotz liefert der obige Algorithmus gute Ergebnisse. Hier ist mal ein Ausgabebeispiel: