August 2018 – Data Science Blog

Funktionsweise künstlicher neuronaler Netze

August 31, 2018/2 Comments/in Artificial Intelligence, Business Analytics, Data Science, Deep Learning, Machine Learning, Main Category, Mathematics /by Benjamin Aunkofer

Künstliche neuronale Netze sind ein Spezialbereich des maschinellen Lernens, der sogar einen eigenen Trendbegriff hat: Deep Learning.
Doch wie funktioniert ein künstliches neuronales Netz überhaupt? Und wie wird es in Python realisiert? Dies ist Artikel 2 von 6 der Artikelserie –Einstieg in Deep Learning.

Gleich vorweg, wir beschränken uns hier auf die künstlichen neuronalen Netze des überwachten maschinellen Lernens. Dafür ist es wichtig, dass das Prinzip des Trainings und Testens von überwachten Verfahren verstanden ist. Künstliche neuronale Netze können aber auch zur unüberwachten Dimensionsreduktion und zum Clustering eingesetzt werden. Das bekannteste Verfahren ist das AE-Net (Auto Encoder Network), das hier aus der Betrachtung herausgenommen wird.

Beginnen wir mit einfach künstlichen neuronalen Netzen, die alle auf dem Perzeptron als Kernidee beruhen. Das Vorbild für künstliche neuronale Netze sind natürliche neuronale Netze, wie Sie im menschlichen Gehirn zu finden sind.

Perzeptron

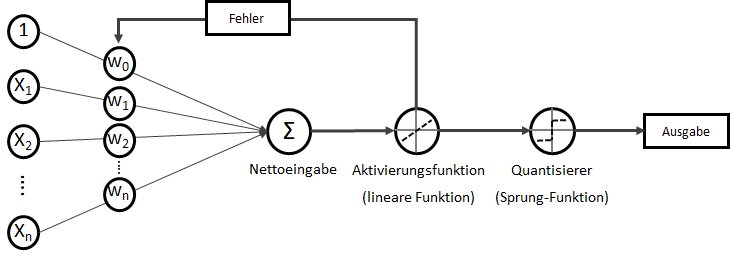
Das Perzeptron (engl. Perceptron) ist ein „Klassiker“ unter den künstlichen neuronalen Netzen. Wenn von einem neuronalen Netz gesprochen wird, ist meistens ein Perzeptron oder eine Variation davon gemeint. Perzeptrons sind mehrschichtige Netze ohne Rückkopplung, mit festen Eingabe- und Ausgabeschichten. Es gibt keine absolut einheitliche Definition eines Perzeptrons, in der Regel ist es jedoch ein reines FeedForward-Netz mit einer Input-Schicht (auch Abtast-Schicht oder Retina genannt) mit statisch oder dynamisch gewichteten Verbindungen zur Ausgabe-Schicht, die (als Single-Layer-Perceptron) aus einem einzigen Neuron besteht. Das eine Neuron setzt sich aus zwei mathematischen Funktionen zusammen: Einer Berechnung der Nettoeingabe und einer Aktivierungsfunktion, die darüber entscheidet, ob die berechnete Nettoeingabe im Brutto nun “feuert” oder nicht. Es ist in seiner Ausgabe folglich binär: Man kann es sich auch als kleines Lämpchen vorstellen, so dass abhängig von den Eingabewerten und den Gewichtungen eine Nettoeingabe (Summe) bildet und eine Sprungfunktion darüber entscheidet, ob am Ende das Lämpchen leuchtet oder nicht. Dieses Konzept der Ausgabeerzeugung wird Forward-Propagation genannt.

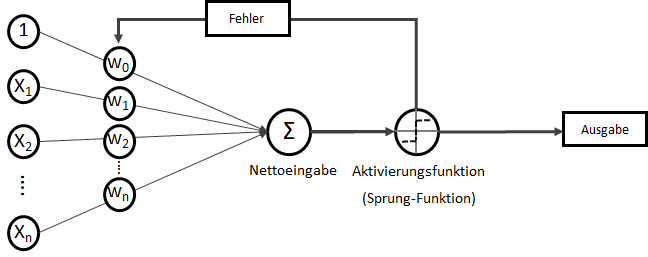
Single-Layer-Perceptron

Auch wenn “Netz” für ein einzelnes Perzeptron mit seinem einen Neuron etwas übertrieben wirken mag, ist es doch die Grundlage für viele größere und mehrschichtige Netze.

Betrachten wir nun die Mathematik der Forward-Propagation.

Wir haben eine Menge an Eingabewerten $x_0, x_1 \dots x_n$ . Wobei für $x_0$ als Bias-Input stets gilt: $x_0 = 1,0$ . Der Bias-Input ist nur ein Platzhalter für das wichtige Bias-Gewicht.

$x = \begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3\\ \vdots\\ x_n \end{bmatrix}$

Für jede Eingabevariable wird eine Gewichtsvariable benötigt: $w_0, w_1 \dots w_n$

$w = \begin{bmatrix} w_0\\ w_1\\ w_2\\ w_3\\ \vdots\\ w_n \end{bmatrix}$

Jedes Produkt aus Eingabewert und Gewichtung soll in Summe die Nettoeingabe $z$ bilden. Hier zeigt sich $z$ als lineare mathematische Funktion, die zwei-dimensional leicht als $z = w_0 + w_1 \cdot x_1$ mit $w_0$ als Y-Achsenschnitt wenn $x_1 = 0$ .

$z = w_0 \cdot x_0 + w_1 \cdot x_1 + \dots + w_n \cdot x_n$

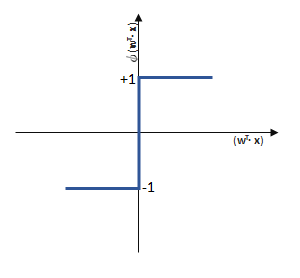
Die lineare Funktion wird nur durch die Sprungfunktion als sogenannte Aktivierungsfunktion zu einer binären Klasseneinteilung (siehe hierzu: Machine Learning – Regression vs Klassifikation), denn wenn $z$ einen festzulegenden Schwellwert $\theta$ überschreitet, liefert die Sprungfunktion $\phi$ mit der Eingabe $z$ einen anderen Wert als wenn dieser Schwellwert nicht überschritten wird.

(1) $\begin{equation*} \phi(z) = \begin{cases} 1 & \text{wenn } z \le \theta \\ -1 & \text{wenn } z < \theta \\ \end{cases} \end{equation*}$

Die Definition dieser Aktivierungsfunktion ist der Kern der Klassifikation und viele erweiterte künstliche neuronale Netze unterscheiden sich im Wesentlichen vom Perzeptron dadurch, dass die Aktivierungsfunktion komplexer ist, als eine reine Sprungfunktion, beispielsweise als Sigmoid-Funktion (basierend auf der logistischen Funktion) oder die Tangens hyperbolicus (tanh) -Funktion. Mehr darüber dann im nächsten Artikel dieser Artikelserie, bleiben wir also bei der einfachen Sprungfunktion.

Künstliche neuronale Netze sind im Grunde nichts anderes als viel-dimensionale, mathematische Funktionen, die durch Schaltung als Neuronen nebeneinander (Neuronen einer Schicht) und hintereinander (mehrere Schichten) eine enorme Komplexität erfassen können. Die Gewichtungen sind dabei die Stellschraube, die die Form der mathematischen Funktion gestaltet, aus Geraden und Kurven, um eine Punktwolke zu beschreiben (Regression) oder um Klassengrenzen zu identifizieren (Klassifikation).

Eine andere Sichtweise auf künstliche neuronale ist die des Filters: Ein künstliches neuronales Netz nimmt alle Eingabe-Variablen entgegen (z. B. alle Pixel eines Bildes) und über ein Training werden die Gewichtungen (die Form des Filters) so gestaltet, dass der Filter immer zu richtigen Klasse (im Kontext der Bildklassifikation: die Objektklasse) führt.

Kommen wir nochmal kurz zurück zu der Berechnung der Nettoeingabe $z$ . Da diese Schreibweise…

$z = w_0 \cdot x_0 + w_1 \cdot x_1 + \dots + w_n \cdot x_n$

… recht anstrengend ist, schreiben Fortgeschrittene der linearen Algebra lieber $z = w^T \cdot x$ .

$z = w^T \cdot x$

Das hochgestellte $T$ steht dabei für transponieren. Transponieren bedeutet, dass Spalten zu Zeilen werden – oder umgekehrt.

Beispielsweise befüllen wir zwei Vektoren $x$ und $w$ mit beispielhaften Inhalten:

Eingabewerte:

$x = \begin{bmatrix} 5\\ 12\\ 30\\ 2 \end{bmatrix}$

Gewichtungen:

$w = \begin{bmatrix} 1\\ 2\\ 5\\ 12 \end{bmatrix}$

Kann nun die Nettoeingabe $z$ berechnet werden, denn der Gewichtungsvektor wird vom Spaltenvektor zum Zeilenvektor. So kann – mathematisch korrekt dargestellt – jedes Element des einen Vektors mit dem zugehörigen Element des anderen Vektors multipliziert werden, die dabei entstehenden Ergebniswerte werden summiert.

$z = w^T \cdot x = \big[1\text{ }2\text{ }5\text{ }12\big] \cdot \begin{bmatrix} 5\\ 12\\ 30\\ 2 \end{bmatrix} = 1 \cdot 5 + 2 \cdot 12 + 5 \cdot 30 + 12 \cdot 2 = 203$

Zurück zur eigentlichen Aufgabe des künstlichen neuronalen Netzes: Klassifikation! (Regression, Clustering und Dimensionsreduktion blenden wir ja in diesem Artikel als Aufgabe aus 🙂

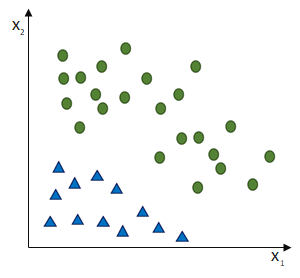
Das Perzeptron soll zwei Klassen trennen. Dafür sollen alle Eingaben richtig gewichtet werden, so dass die entstehende Nettoeingabe $z$ die Sprungfunktion dann aktiviert, wenn der Datensatz nicht für die eine, sondern für die andere Klasse ausweist.

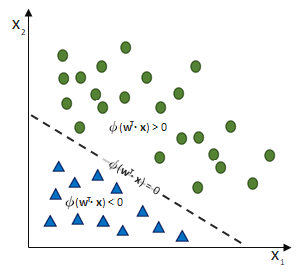Da wir es mit einer linearen Funktion $z$ zutun haben, ist die Konvergenz (= Passgenauigkeit des Models mit der Realität) eines Single-Layer-Perzeptrons nur für lineare Trennbarkeit möglich!

Training des Perzeptron-Netzes

Die Aufgabe ist nun, die richtigen Gewichte zu finden – und nicht nur irgendwelche richtigen, sondern genau die optimalen. Die Frage, die sich für jedes künstliche neuronale Netz stellt, ist die nach den richtigen Gewichtungen. Das Training eines Perzeptron ist vergleichsweise einfach, gerade weil es binär ist. Denn binär bedeutet auch, dass wenn eine falsche Antwort gegeben wurde, muss das jeweils andere mögliche Ergebnis korrekt sein.

Das Training eines Perzeptrons funktioniert wie folgt:

Setze alle Gewichtungen auf den Wert 0,00
Mit jedem Datensatz des Trainings
1. Berechne den Ausgabewert $\^{y}$
2. Vergleiche den Ausgabewert $\^{y}$ mit dem tatsächlichen Ergebnis $y$
3. Aktualisiere die Gewichtungen entgegen des Fehlers: $w_i = w_i + \Delta w_i$

Wobei die Gewichtsanpassung $\Delta w_i$ entgegen des Fehlers (bzw. hin zur jeweils anderen möglichen Antwort) geschieht:

$\Delta w_i = (\^{y}_j - y_j ) \cdot x_i$

Anmerkung für die Experten: Die Schrittweite $\eta$ blenden wir hier einfach mal aus. Bitte einfach von $\eta = 1.0$ ausgehen.

$\Delta w_i$ ist die Differenz aus der Prädiktion und dem tatsächlichen Ergebnis (Klasse). Alle Gewichtungen werden mit jedem Fehler gleichzeitig aktualisiert. Sind alle Gewichtungen aktualisiert, kommt der nächste Durchlauf (erneuter Vergleich zwischen $\^{y}$ und $y$ ), nicht zu vergessen ist dabei natürlich die Abhängigkeit von den Eingabewerten x:

$\Delta w_0 = (\^{y}_j - y_j ) \cdot x_0$

$\Delta w_2 = (\^{y}_j - y_j ) \cdot x_1$

$\Delta w_2 = (\^{y}_j - y_j) \cdot x_2$

$\Delta w_n = (\^{y}_j - y_j) \cdot x_n$

Training eines Perzeptrons

Das Training im überwachten Lernen basiert immer auf der Idee, den Ausgabe-Fehler (die Differenz zwischen Prädiktion und tatsächlich korrektem Ergebnis) zu betrachten und die Klassifikationslogik an den richtigen Stellschrauben (bei neuronalen Netzen sind das die Gewichtungen) entgegen des Fehlers anzupassen.

Richtige Klassifikations-Situationen können True-Positives und True-Negatives darstellen, die zu keiner Gewichtsanpassung führen sollen:

True-Positive -> Klassifikation: 1 | korrekte Klasse: 1

$\Delta w_i = (\^{y}_j - y_j) \cdot x_i = (1 - 1) \cdot x_i = 0$

True-Negative-> Klassifikation: -1 | korrekte Klasse: -1

$\Delta w_i = (\^{y}_j - y_j) \cdot x_i = (-1 - -1) \cdot x_i = 0$

Falsche Klassifikationen erzeugen einen Fehler, der zu einer Gewichtsanpassung entgegen des Fehlers führen soll:

False-Positive -> Klassifikation: 1 | korrekte Klasse: -1

$\Delta w_i = (\^{y}_j - y_j) \cdot x_i = (1 - -1) \cdot x_i = 2 \cdot x_i$

False-Negative -> Klassifikation: -1 | korrekte Klasse: 1

$\Delta w_i = (\^{y}_j - y_j) \cdot x_i = (-1 - 1) \cdot x_i = -2 \cdot x_i$

Imaginäres Trainingsbeispiel eines Single-Layer-Perzeptrons (SLP)

Nehmen wir an, dass $x_1 = 0,5$ ist und das SLP irrtümlicherweise die Klasse $\^{y_1} = -1$ ausgewiesen hat, obwohl die korrekte Klasse $y_1 = +1$ wäre. (Und die Schrittweite lassen wir bei $\eta = 1,0$ )

Dann passiert folgendes:

$\Delta w_1 = (\^{y}_1 - y_1) \cdot x_1 = (-1 - 1) \cdot 0,5 = -2,0 \cdot 0,5 = -1,0$

Die Gewichtung $w_1$ verringert sich entsprechend $w_1 = w_1 + \Delta w_1 = w_1 - 1,0$ und somit wird die Wahrscheinlichkeit größer, dass wenn bei der nächsten Iteration ( $j=1$ ) wieder die Klasse +1 korrekt sei, den Schwellwert $\phi(z)$ zu unterschreiten und auf eben diese korrekte Klasse zu stoßen.

Die Aktualisierung der Gewichtung $\Delta w_i$ ist proportional zu $x_i$ . So würde beispielsweise ein neues $x_1=2,0$ (bei Iteration $j=2$ ) zu einer irrtümlichen Klassifikation $\^(y_2) = -1$ ( $y_2 = +1$ ) führen, würde die Entscheidungsgrenze zur korrekten Prädiktion der Klasse beim nächsten Durchlauf ( $j = 3$ ) an $w_1$ noch weiter in die gleiche Richtung verschoben werden:

$\Delta w_1 = (\^{y}_2 - y_2) \cdot x_1 = (-1 - 1) \cdot 2,0 = -2,0 \cdot 2,0 = -4,0$

Mehr zum Training von künstlichen neuronalen Netzen ist im nächsten Artikel dieser Artikelserie zu erfahren.

Single-Layer-Perzeptrons (SLP) – Beispiel mit der boolischen Trennung

Verlassen wir nun das Training des Perzeptrons und gehen einfach mal davon aus, dass die idealen Gewichte schon gefunden wurden und schauen uns nun an, was ein Perzeptron alles (nicht) kann. Denn nicht vergessen, es soll eigentlich Klassen unterscheiden bzw. die dafür nötigen Entscheidungsgrenzen finden.

Boolische Operatoren unterscheiden Fälle nach boolischen Werten. Sie sind ein beliebtes “Hello World” für die Einarbeitung in die lineare Entscheidungslogik eines Perzeptrons. Es gibt drei grundlegende boolische Vergleichsoperatoren: AND, OR und XOR

x1	x2	AND	OR	XOR
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

Ein Perzeptron zur Lösung dieser Aufgabe bräuchte also zwei Dimensionen (+ Bias): $x_1$ und $x_2$
Und es müsste Gewichtungen haben, die dafür sorgen, dass die Vorhersage entsprechend der Logik AND, OR oder XOR mit $\^{y} = \phi(z) = \phi (w_0 \cdot 1 + w_1 \cdot x_1 + w_2 \cdot x_2)$ funktioniert.

Dabei ist es wichtig, dass wir auch phi $\phi$ als Sprungfunktion definieren. Sie könnte beispielsweise so aussehen, dass sie auf den Wert $\phi(z) = 1$ springt, wenn z > 0 ist, ansonsten aber $\phi(z) = 0$ bleibt.

Das Netz und die Gewichtungen (w-Setup) könnten für die AND- und die OR-Logik so aussehen:

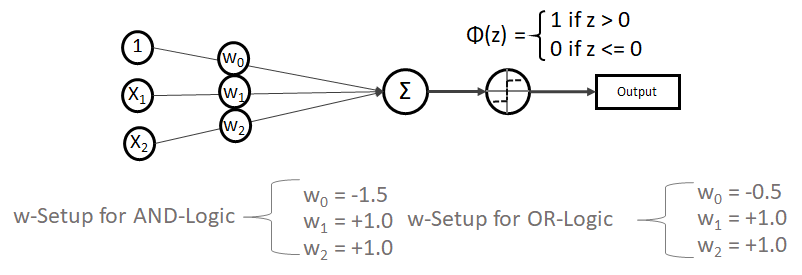
Die Gewichtungen funktionieren beim SLP problemlos, denn wir haben es mit linear trennbaren Problemen zutun:

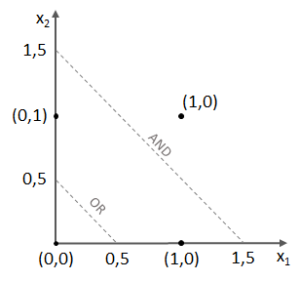
Kleiner Test gefällig? So nehmen wir uns erstmal die AND-Logik vor:

Wenn x1 = 0 und x2 = 0 ist, gilt: $z = -1,5 \cdot 1 + 1 \cdot 0 + 1 \cdot 0 = - 1,5$ ,
wie erhalten als Prädiktion $\phi(z) = \phi(-1,5) = 0$
Wenn x1 = 1 und x2 = 0 ist, gilt: $z = -1,5 \cdot 1 + 1 \cdot 1 + 1 \cdot 0 = - 0,5$ ,
wie erhalten als Prädiktion $\phi(z) = \phi(-0,5) = 0$
Wenn x1 = 1 und x2 = 1 ist, gilt: $z = -1,5 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 = + 0,5$ ,
wie erhalten als Prädiktion $\phi(z) = \phi(0,5) = 1$

Scheint zu funktionieren!

Und dann die OR-Logik mit

Wenn x1 = 0 und x2 = 0 ist, gilt: $z = -0,5 \cdot 1 + 1 \cdot 0 + 1 \cdot 0 = - 0,5$ ,
wie erhalten als Prädiktion $\phi(z) = \phi(-0,5) = 0$
Wenn x1 = 1 und x2 = 0 ist, gilt: $z = -0,5 \cdot 1 + 1 \cdot 1 + 1 \cdot 0 = + 0,5$ ,
wie erhalten als Prädiktion $\phi(z) = \phi(0,5) = 1$
Wenn x1 = 1 und x2 = 1 ist, gilt: $z = -0,5 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 = + 1,5$ ,
wie erhalten als Prädiktion $\phi(z) = \phi(1,5) = 1$

Super! Jedoch stellt sich nun die Frage, wie das XOR-Problem zu lösen ist, denn das bedingt sowohl die Grenzen von AND als auch jene des OR-Operators.

Multi-Layer-Perzeptron (MLP) bzw. (Deep) Feed Forward (FF) Net

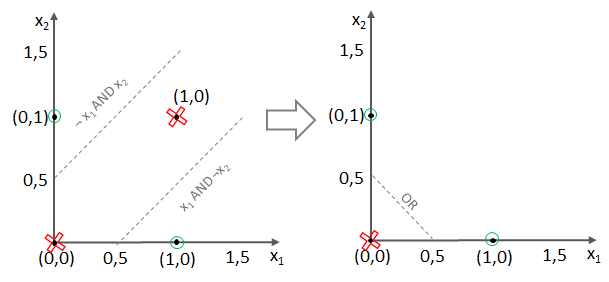
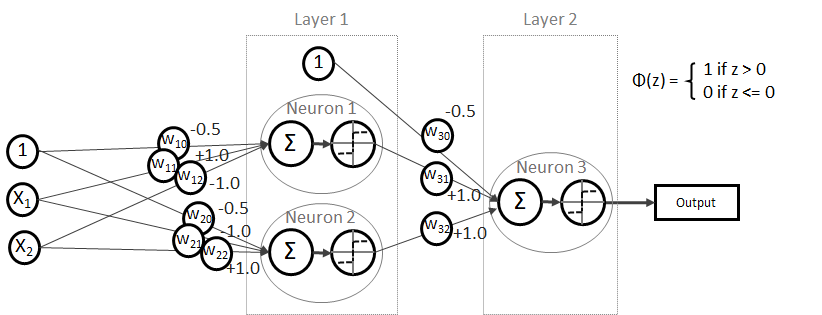
Denn ein XOR kann mathematisch auch so korrekt beschrieben werden: $x_1 \text{ xor } x_2 = (x_1 \text{ and } \neg x_2) \text{ or } (\neg x_1 \text{ and } x_2)$

Testen wir es aus!

Wenn x1 = 0 und x2 = 0 ist, gilt:
$z_1 = w_{10} \cdot 1 + w_{11} \cdot x1 + w_{12} \cdot x2 = -0.5 \cdot 1 + 1,0 \cdot 0 - 1,0 \cdot 0 = -0,5$ und somit $\phi(z_1) = \phi(-0,5) = 0$
$z_2 = w_{20} \cdot 1 + w_{21} \cdot x1 + w_{22} \cdot x2 = -0.5 \cdot 1 - 1,0 \cdot 0 + 1,0 \cdot 0 = -0,5$ und somit $\phi(z_2) = \phi(-0,5) = 0$
$z_3 = w_{30} \cdot 1 + w_{31} \cdot \phi(z_1) + w_{32} \cdot \phi(z_2) = -0,5 \cdot 1 + 1,0 \cdot 0 + 1,0 \cdot 0 = -0,5$ und somit $\phi(z_3) = \phi(-0,5) = 0$
Wenn x1 = 1 und x2 = 0 ist, gilt:
$z_1 = w_{10} \cdot 1 + w_{11} \cdot x1 + w_{12} \cdot x2 = -0.5 \cdot 1 + 1,0 \cdot 1 - 1,0 \cdot 0 = 0,5$ und somit $\phi(z_1) = \phi(0,5) = 1$
$z_2 = w_{20} \cdot 1 + w_{21} \cdot x1 + w_{22} \cdot x2 = -0.5 \cdot 1 - 1,0 \cdot 1 + 1,0 \cdot 0 = -1,5$ und somit $\phi(z_2) = \phi(-1,5) = 0$
$z_3 = w_{30} \cdot 1 + w_{31} \cdot \phi(z_1) + w_{32} \cdot \phi(z_2) = -0,5 \cdot 1 + 1,0 \cdot 1 + 1,0 \cdot 0 = 0,5$ und somit $\phi(z_3) = \phi(0,5) = 1$
Wenn x1 = 0 und x2 = 1 ist, gilt:
$z_1 = w_{10} \cdot 1 + w_{11} \cdot x1 + w_{12} \cdot x2 = -0.5 \cdot 1 + 1,0 \cdot 0 - 1,0 \cdot 1 = -1,5$ und somit $\phi(z_1) = \phi(-1,5) = 0$
$z_2 = w_{20} \cdot 1 + w_{21} \cdot x1 + w_{22} \cdot x2 = -0.5 \cdot 1 - 1,0 \cdot 0 + 1,0 \cdot 1 = 0,5$ und somit $\phi(z_2) = \phi(0,5) = 1$
$z_3 = w_{30} \cdot 1 + w_{31} \cdot \phi(z_1) + w_{32} \cdot \phi(z_2) = -0,5 \cdot 1 + 1,0 \cdot 0 + 1,0 \cdot 1 = 0,5$ und somit $\phi(z_3) = \phi(0,5) = 1$
Wenn x1 = 1 und x2 = 1 ist, gilt:
$z_1 = w_{10} \cdot 1 + w_{11} \cdot x1 + w_{12} \cdot x2 = -0.5 \cdot 1 + 1,0 \cdot 1 - 1,0 \cdot 1 = -1,5$ und somit $\phi(z_1) = \phi(-0,5) = 0$
$z_2 = w_{20} \cdot 1 + w_{21} \cdot x1 + w_{22} \cdot x2 = -0.5 \cdot 1 - 1,0 \cdot 1 + 1,0 \cdot 1 = 0,5$ und somit $\phi(z_2) = \phi(-0,5) = 0$
$z_3 = w_{30} \cdot 1 + w_{31} \cdot \phi(z_1) + w_{32} \cdot \phi(z_2) = -0,5 \cdot 1 + 1,0 \cdot 0 + 1,0 \cdot 0 = -0,5$ und somit $\phi(z_3) = \phi(-0,5) = 0$

Es funktioniert!

Mehrfachklassifikation mit dem Perzeptron

Ein Perzeptron-Netz klassifiziert binär, die Ausgabe beschränkt sich auf 1 oder -1 bzw. 0 oder 1.

Jedoch wird in der Praxis oftmals eine One-vs-All (OvA) bzw. One-vs-Rest (OvR) Klassifikation implementiert. In diesem Fall steht die 1 für die Erkennung einer konkreten Klasse, während alle anderen übrigen Klassen als negativ betrachtet werden.

Um jede Klasse erkennen zu können, werden n Klassifizierer (= n Perzeptron-Netze) benötigt. Jedes Perzeptron-Netz ist auf die Erkennung einer bestimmten Klasse trainiert.

Adaline – Oder: die Limitation des Perzeptrons

Das Perzeptron wird nur über eine Sprungfunktion aktiviert. Das schränkt die Feinabstimmung des Trainings enorm ein. Besser sind Aktivierungen über stetige Funktionen, die dann nämlich differenzierbar (ableitbar) sind. Das ergibt eine konvexe Fehlerfunktion mit einem eindeutigen Minimum. Der Adaline-Algorithmus (ADAptive Linear NEuron) erweitert die Idee des Perzeptrons um genau diese Idee. Der wesentliche Fortschritt der Adaline-Regel gegenüber der des Perzeptrons ist demnach, dass die Aktualisierung der Gewichtungen nicht wie beim Perzeptron auf einer einfachen Sprungfunktion, sondern auf einer linearen, stetigen Aktivierungsfunktion beruht.

Single-Layer-Adaline

Wie ein künstliches neuronales Netz mit der Kategorie Adaline trainiert werden kann, wird im nächsten Artikel dieser Artikelserie erläutert.

Weiterführende Netz-Konzepte (CNN und RNN)

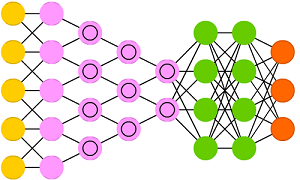
Wer bereits mit Frameworks wie TensorFlow in das Deep Learning eingestiegen ist, hat möglicherweise schon erweiterte Konzepte der künstlichen neuronalen Netze kennen gelernt. Die CNNs (Convolutional Neuronal Network) sind im Moment die Wahl für die Verarbeitung von hochdimensionalen Aufgaben, beispielsweise die Bilderkennung (Computer Vision) und Texterkennung (NLP). Das CNN erweitert die Möglichkeiten mit neuronalen Netzen deutlich, indem ein Netz zur Dimensionsreduktion vorgeschaltet wird, im Kern steckt jedoch weiterhin die Idee der MLPs. Beim Einsatz in der Bilderkennung funktionieren CNNs vereinfacht gesprochen so, dass der vorgeschaltete Netzbereich die Millionen Bildpixel sektorweise ausliest (Convolution, Faltung durch Auslesen über Sektoren, die sich gegenseitig überlappen), verdichtet (Pooling, beispielsweise über nicht-lineare Funktionen wie max()) und dann – nach diesem Prozedere – ähnlich eim MLP klassifiziert.

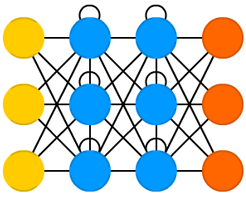
Eine andere erweiterte Form sind RNNs (Recurrent Neuronal Network), die ebenfalls auf der Idee des MLPs basieren, dieses Konzept jedoch dank Rückverbindungen (Neuronen senden an vorherige Schichten) und Selbstverbindungen (Neuronen senden an sich selbst) wiederum auf den Kopf stellen.

Dennoch ist es für das tiefere Verständnis von CNNs und RNNs essenziell, dass vorher das Konzept des MLPs verstanden ist. Es ist die einfachste Form der auch heute noch am meisten eingesetzten und sehr mächtigen Netz-Topologien.

Im Jahr 2016 hatte Fjodor van Veen von asimovinstitute.org hatte – dankenswerterweise – mal eine Zusammenstellung von Netz-Topologien erstellt, auf die ich heute noch immer mal wieder einen Blick werfe:

Künstliche neuronale Netze – Topologie-Übersicht von Fjodor van Veen

Buchempfehlungen

Die folgenden Bücher nutze ich für mein Selbststudium von Machine Learning und Deep Learning und sind teilweise Gedankenvorlagen auch für diesen Artikel gewesen:


Machine Learning mit Python und Scikit-Learn und TensorFlow: Das umfassende Praxis-Handbuch für Data Science, Predictive Analytics und Deep Learning (mitp Professional)	Deep Learning mit Python und Keras: Das Praxis-Handbuch vom Entwickler der Keras-Bibliothek(mitp Professional)

Modelling Data – Case Study: Importance of domain knowledge

August 29, 2018/2 Comments/in Artificial Intelligence, Audit Analytics, Big Data, Data Science, Insights, Machine Learning, Realtime Analytics, Statistics, Use Case /by Marius Schulz

What´s the relation between earnings and happiness? I saw this chart and was strongly irritated – why is there a linear regression, it´s clearly a logarithmic relationship.

So I got angry and wanted to know, which model is the better fit. I started to work immediatly, because it´s a huge difference for man kind. Think about it: you give a poor person money and he gets as happy as a rich person with the same amount added – that´s against common sense and propaganda to get rich. Like an cultural desease.

So I gathered the data and did a first comparation, and this logarithmic model was the better fit:

I was right and seriously willing to clear the mess up – so posted the “correct” model on facebook, to explain things to my friends.

Once I came down…

I asked myself: “What´s the model that fits the data best – that would be more correct?”

So I started to write an algorithm to check polynominal regression levels for fit using a random train and test data split. Finally, I got to this result and was amazed:

This seriously hit me: “What the f***! There seems to be maximum happiness reachable with a certain amount of income / GDP.” Can you understand, what this result would mean for our world and economy? Think about all economies growing continiously, but well happiest was there or will come there. What would you do? Send income to less developed countries, because you don´t need it? Stop invention and progress, because it´s of no use? Seriously, I felt like a socialist: Stop progress at this point and share.

So I thought a while and concluded: “F***ing statistics, we need a profound econometric model.”

I started modelling: Well, the first amount of money in a market based on money leverages a huge amount of happiness, because you can participate and feed yourself. We can approximate that by infinit marginal utility. Then the more you have, the less utility should be provided by the additional same amount added. Finally, more income is more options, so more should be always better. I concluded, that this is catched by a Cobb Douglas production function. Here´s the graph:

That´s it, that´s the final model. Here I feel home, this looks like a normal world – for an economist.

The Relevance of Domain Knowledge

As this short case study shows, we get completly wrong information and conclusions, if we don´t do it right. If you were the most important decision making algorithm in global economic politics, imagine what desasterous outcomes it would have produced to automatically find an optimum of income.

This is a serious border of AI. If you want to analyse Big Data with algorithms, you may produce seriously wrong information and conclusions. Statistical analysis is allways about using the right model. And modelling is about the assumptions of the model. As long as you can not create the right assumtions for the statistical model automatically, Big Data analysis is near to crazy. So out of this point of view, Big Data analysis is either about very simplistic tendencies (like linear trends) or it´s bound to Data Scientists with domain knowledge checking each model – that´s slow.

Discussion

I´m quite new to the field of Data Science, but this case study shows very though limitations, clearly. It´s not about flexible fitting of data, it´s about right models. And right models don´t scale into the Big Data domain. What do you think is the solution for this issue?

Countries of Happiness – the Full Article

If you are interested in my final article on my personal blog, explaining the final results: Please feel welcome to read the article here. There is a translation widget in the menu, to read in your favorite language. The original article is german.

Data Science Survey by lexoro.ai

August 22, 2018/0 Comments/in Carrier, Data Science News, Gerneral, Insights /by Dario Zocholl

Ergebnisse unserer zweiten Data Science Survey

Künstliche Intelligenz, Data Science, Machine Learning – über die Bedeutung dieser Themen für einzelne Unternehmen und Branchen herrscht weiterhin viel Unsicherheit und Unklarheit. Zudem stellt sich die Frage: Welche Fähigkeiten und Kompetenzen braucht ein guter Data Scientist eigentlich?

Es lässt sich kaum bestreiten, dass wir vor einem Paradigmenwechsel stehen, vorangetrieben durch einen technologischen Fortschritt dessen Geschwindigkeit exponentiell zunimmt.
Der Arbeitsmarkt im Speziellen sieht sich auch einem starken Veränderungsprozess unterworfen. Es entstehen neue Jobs, neue Rollen und neue Verantwortungsbereiche. Data Scientist, Machine Learning Expert, RPA Developer – die Trend-Jobs der Stunde. Aber welche Fähigkeiten und Skills verbergen sich eigentlich hinter diesen Jobbeschreibungen? Hier scheint es noch eine große Divergenz zu geben.

Unser zweiter Data Science Leaks-Survey soll hier für mehr Transparenz und Aufklärung sorgen. Die Ergebnisse fließen zudem in die Entwicklung unseres SkillPrint ein, einer individuellen Analyse der Kompetenzen eines jeden Daten-Experten. Eine erste Version davon wird in Kürze fertiggestellt sein.

Link zu den Ergebnissen der zweiten Data Science Survey by lexoro.ai

Viel Spaß beim Lesen unserer Ministudie zum Thema: Data Science… mehr als Python, TensorFlow & Neural Networks

Interesse an einem Austausch zu verschiedenen Karriereperspektiven im Bereich Data Science/ Machine Learning? Dann registrieren Sie sich direkt auf dem lexoro Talent Check-In und ein lexoro-Berater wird sich bei Ihnen melden.

Interview – Nutzen und Motivation der medizinischen Datenanalyse

August 16, 2018/0 Comments/in Carrier, Certification / Training, Data Science News, Education / Certification, Gerneral, Insights, Interviews /by Benjamin Aunkofer

Interview mit Prof. Thomas Schrader zur Motivation des Erlernens von Clinical Data Analytics

Prof. Dr. Thomas Schrader ist Fachbereichsleiter Informatik und Medien an der TH Brandenburg und hat seinen Projekt- und Lehrschwerpunkt in der Medizininformatik. Als Experte für Data Science verknüpft er das Wissen um Informatik und Statistik mit einem medizinischen Verständnis. Dieses Wissen wird genutzt, um eine beweisorientierte Diagnose stellen, aber auch, um betriebswirtschaftliche Prozesse zu verbessern. Prof. Thomas Schrader ist zudem Dozent und Mitgestalter des Zertifikatskurses Clinical Data Analytics.

Data Science Blog: Wie steht es um die medizinische Datenanalyse? Welche Motivation gibt es dafür, diese zu erlernen und anzuwenden?

Die Digitalisierung ist inzwischen auch in der Medizin angekommen. Befunde, Laborwerte und Berichte werden elektronisch ausgetauscht und stehen somit digital zur Verfügung. Ob im Krankenhaus, im Medizinischen Versorgungszentrum oder in der ambulanten Praxis, medizinische Daten dienen zur Befunderhebung, Diagnosestellung oder zur Therapiekontrolle.

Über mobile Anwendungen, Smart Phones und Smart Watches werden ebenfalls Daten erhoben und PatientInnen stellen diese zur Einsicht zur Verfügung.

Die Verwaltung der Daten und die richtige Nutzung der Daten wird zunehmend zu einer notwendigen Kompetenz im medizinischen Berufsalltag. Jetzt besteht die Chance, den Umgang mit Daten zu erlernen, deren Qualität richtig zu beurteilen und den Prozess der fortschreitenden Digitalisierung zu gestalten.

Daten haben Eigenschaften, Daten haben eine Lebenszeit, einen Lebenszyklus. Ähnlich einem Auto, sind verschiedene Personen in unterschiedlichen Rollen daran beteiligt und verantwortlich , Daten zu erheben, zu speichern oder Daten zur Verfügung zu stellen. Je nach Art der Daten, abhängig von der Datenqualität lassen sich diese Daten weiterverwenden und ggf. Schlussfolgerungen ziehen. Die Möglichkeit aus Daten Wissen zu generieren, ist für die medizinische Arbeit eine große Chance und Herausforderung.

Data Science Blog: Bedeutet MDA gleich BigData?

Big Data ist inzwischen ein Buzzwort: Alles soll mit BigData und der Anwendung von künstlicher Intelligenz gelöst werden. Es entsteht aber der Eindruck, dass nur die großen Firmen (Google, Facebook u.a.) von BigData profitieren. Sie verwenden ihre Daten, um Zielgruppen zu differenzieren, zu identifizieren und Werbung zu personalisieren.

Medizinische Datenanalyse ist nicht BigData! Medizinische Datenanalyse kann lokal mit den Daten eines Krankenhauses, eines MVZ oder ambulanten Praxis durchgeführt werden. Explorativ wird das Wissen aus diesen Daten erschlossen. Es können schon auf dieser Ebene Indikatoren der medizinischen Versorgung erhoben werden. Es lassen sich Kriterien berechnen, die als Indikatoren für die Detektion von kritischen Fällen dienen.

Mit einer eigenen Medizinischen Datenanalyse lassen sich eigene Daten analysieren, ohne jemals die Kontrolle über die Daten abzugeben. Es werden dabei Methoden verwendet, die teilweise auch bei Big Data Anwendung finden.

Data Science Blog: Für wen ist das Erlernen der medizinischen Datenanalyse interessant?

Die Medizinische Datenanalyse ist für alle interessant, die sich mit Daten und Zahlen in der Medizin auseinandersetzen. Die Frage ist eigentlich, wer hat nichts mit Daten zu tun?

Im ersten Augenblick fallen die ambulant und klinisch tätigen ÄrztInnen ein, für die MDA wichtig wäre: in einer Ambulanz kommt ein für diese Praxis typisches Spektrum an PatientInnen mit ihren Erkrankungsmustern. MDA kann diese spezifischen Eigenschaften charakterisieren, denn darin liegt ja Wissen: Wie häufig kommen meine PatientInnen mit der Erkrankung X zu mir in die Praxis? Dauert bei einigen PatientInnen die Behandlungszeit eigentlich zu lange? Bleiben PatientInnen weg, obwohl sie noch weiter behandelt werden müssten? Dahinter liegen also viele Fragen, die sich sowohl mit der Wirtschaftlichkeit als auch mit der Behandlungsqualität auseinandersetzen. Diese sehr spezifischen Fragen wird Big Data übrigens niemals beantworten können.

Aber auch die Pflegekräfte benötigen eigentlich dringend Werkzeuge für die Bereitstellung und Analyse der Pflegedaten. Aktuell wird sehr über die richtige Personalbesetzung von Stationen und Pflegeeinrichtungen diskutiert. Das eigentliche Problem dabei ist, dass für die Beantwortung dieser Frage Zahlen notwendig sind: über dokumentierte Pflegehandlungen, Arbeitszeiten und Auslastung. Inzwischen wird damit begonnen, dieses Daten zu erheben, aber es fehlen eine entsprechende Infrastruktur dieses Daten systematisch zu erfassen, auszuwerten und in einen internationalen, wissenschaftlichen Kontext zu bringen. Auch hier wird Big Data keine Erkenntnisse bringen: weil keine Daten vorhanden sind und weil keine ExpertIn aus diesem Bereich die Daten untersucht.

Die Physio-, ErgotherapeutInnen und LogopädInnen stehen aktuell unter dem hohen Druck, einen Nachweis ihrer therapeutischen Intervention zu bringen. Es geht auch hier schlicht darum, ob auch zukünftig alle Therapieformen bezahlt werden. Über die Wirksamkeit von Physio-, Ergo- und Logopädie können nur Statistiken Auskunft geben. Auch diese Berufsgruppen profitieren von der Medizinischen Datenanalyse.

In den Kliniken gibt es Qualitäts- und Risikomanager. Deren Arbeit basiert auf Zahlen und Statistiken. Die Medizinische Datenanalyse kann helfen, umfassender, besser über die Qualität und bestehende Risiken Auskunft zu geben.

Data Science Blog: Was kann genau kann die medizinische Datenanalyse leisten?

Die Technische Hochschule Brandenburg bietet einen Kurs Medizinische/ Klinische Datenanalyse an. In diesem Kurs wird basierend auf dem Lebenszyklus von Daten vermittelt, welche Aufgaben zu leisten sind, um gute Analysen durchführen zu können. Das fängt bei der Datenerhebung an, geht über die richtige und sichere Speicherung der Daten unter Beachtung des Datenschutzes und die Analyse der Daten. Da aber gerade im medizinischen Kontext die Ergebnisse eine hohe Komplexität aufweisen können, kommt auch der Visualisierung und Präsentation von Daten eine besondere Bedeutung zu. Eine zentrale Frage, die immer beantwortet werden muss, ist, ob die Daten für bestimmte Aussagen oder Entscheidungen tauglich sind. Es geht um die Datenqualität. Dabei ist nicht immer die Frage zu beantworten, ob das “gute” oder “schlechte” Daten sind, sondern eher um die Beschreibung der spezifischen Eigenschaften von Daten und die daraus resultierenden Verwendungsmöglichkeiten.

Data Science Blog: Sie bieten an der TH Brandenburg einen Zertifikatskurs zum Erlernen der Datenanalyse im Kontext der Medizin an. Was sind die Inhalte des Kurses?

Der Kurs gliedert sich in drei Module:

– Modul 1 – Daten aus Klinik und Pflege – Von den Daten zur Information: In diesem Modul wird auf die unterschiedlichen Datenquellen eingegangen und deren Qualität näher untersucht. Daten allein sagen zuweilen sehr wenig, sie müssen in einen Zusammenhang gebracht werden, damit daraus verwertbare Informationen. Im Mittelpunkt stehen die Teile des Datenlebenszyklus, die sich mit der Erhebung und Speicherung der Daten beschäftigen.

– Modul 2 – Anwenden der Werkzeuge: Analysieren, Verstehen und Entscheiden – Von Information zum Wissen. Der Schritt von Information zu Wissen wird dann begangen, wenn eine Strukturierung und Analyse der Informationen erfolgt: Beschreiben, Zusammenfassen und Zusammenhänge aufdecken.

– Modul 3 – Best practice – Fallbeispiele: Datenanalyse für die Medizin von morgen – von smart phone bis smart home, von Registern bis sozialen Netzen: In diesem Modul wird an Hand von verschiedenen Beispielen der gesamte Datenlebenszyklus dargestellt und mit Analysen sowie Visualisierung abgeschlossen.

Data Science Blog: Was unterscheidet dieser Kurs von anderen? Und wie wird dieser Kurs durchgeführt?

Praxis, Praxis, Praxis. Es ist ein anwendungsorientierter Kurs, der natürlich auch seine theoretische Fundierung erhält aber immer unter dem Gesichtspunkt, wie kann das theoretische Wissen direkt für die Lösung eines Problems angewandt werden. Es werden Problemlösungsstrategien vermittelt, die dabei helfen sollen verschiedenste Fragestellung in hoher Qualität aufarbeiten zu können.

In wöchentlichen Online-Meetings wird das Wissen durch Vorlesungen vermittelt und in zahlreichen Übungen trainiert. In den kurzen Präsenzzeiten am Anfang und am Ende eines Moduls wird der Einstieg in das Thema gegeben, offene Fragen diskutiert oder abschließend weitere Tipps und Tricks gezeigt. Jedes Modul wird mit einer Prüfung abgeschlossen und bei Bestehen vergibt die Hochschule ein Zertifikat. Für den gesamten Kurs gibt es dann das Hochschulzertifikat „Clinical Data Analyst“.

Der Zertifikatskurs „Clinical Data Analytics“ umfasst die Auswertung von klinischen Daten aus Informationssystemen im Krankenhaus und anderen medizinischen und pflegerischen Einrichtungen. Prof. Thomas Schrader ist einer der Mitgestalter des Kurses. Weitere Informationen sind stets aktuell auf www.th-brandenburg.de abrufbar.

How To Remotely Send R and Python Execution to SQL Server from Jupyter Notebooks

August 13, 2018/1 Comment/in Data Mining, Data Science, Data Science Hack, Data Warehousing, Database, Main Category, Python, Python, R Statistics, SQL, Tools, Tutorial /by Kyle Weller

Introduction

Did you know that you can execute R and Python code remotely in SQL Server from Jupyter Notebooks or any IDE? Machine Learning Services in SQL Server eliminates the need to move data around. Instead of transferring large and sensitive data over the network or losing accuracy on ML training with sample csv files, you can have your R/Python code execute within your database. You can work in Jupyter Notebooks, RStudio, PyCharm, VSCode, Visual Studio, wherever you want, and then send function execution to SQL Server bringing intelligence to where your data lives.

This tutorial will show you an example of how you can send your python code from Juptyter notebooks to execute within SQL Server. The same principles apply to R and any other IDE as well. If you prefer to learn through videos, this tutorial is also published on YouTube here:

Environment Setup Prerequisites

Install ML Services on SQL Server

In order for R or Python to execute within SQL, you first need the Machine Learning Services feature installed and configured. See this how-to guide.

Install RevoscalePy via Microsoft’s Python Client

In order to send Python execution to SQL from Jupyter Notebooks, you need to use Microsoft’s RevoscalePy package. To get RevoscalePy, download and install Microsoft’s ML Services Python Client. Documentation Page or Direct Download Link (for Windows).

After downloading, open powershell as an administrator and navigate to the download folder. Start the installation with this command (feel free to customize the install folder): .\Install-PyForMLS.ps1 -InstallFolder “C:\Program Files\MicrosoftPythonClient”

Be patient while the installation can take a little while. Once installed navigate to the new path you installed in. Let’s make an empty folder and open Jupyter Notebooks: mkdir JupyterNotebooks; cd JupyterNotebooks; ..\Scripts\jupyter-notebook

Create a new notebook with the Python 3 interpreter:

To test if everything is setup, import revoscalepy in the first cell and execute. If there are no error messages you are ready to move forward.

Database Setup (Required for this tutorial only)

For the rest of the tutorial you can clone this Jupyter Notebook from Github if you don’t want to copy paste all of the code. This database setup is a one time step to ensure you have the same data as this tutorial. You don’t need to perform any of these setup steps to use your own data.

Create a database

Modify the connection string for your server and use pyodbc to create a new database.

import pyodbc

# creating a new db to load Iris sample in

new_db_name = "MLRemoteExec" connection_string = "Driver=SQL Server;Server=localhost\MSSQLSERVER2017;Database={0};Trusted_Connection=Yes;"

cnxn = pyodbc.connect(connection_string.format("master"), autocommit=True)

cnxn.cursor().execute("IF EXISTS(SELECT * FROM sys.databases WHERE [name] = '{0}') DROP DATABASE {0}".format(new_db_name))

cnxn.cursor().execute("CREATE DATABASE " + new_db_name)

cnxn.close()

print("Database created")

Import Iris sample from SkLearn

Iris is a popular dataset for beginner data science tutorials. It is included by default in sklearn package.

from sklearn import datasetsimport pandas as pd

# SkLearn has the Iris sample dataset built in to the packageiris = datasets.load_iris()

df = pd.DataFrame(iris.data, columns=iris.feature_names)

Use RecoscalePy APIs to create a table and load the Iris data

(You can also do this with pyodbc, sqlalchemy or other packages)

from revoscalepy import RxSqlServerData, rx_data_step

# Example of using RX APIs to load data into SQL table. You can also do this with pyodbc

table_ref = RxSqlServerData(connection_string=connection_string.format(new_db_name), table="Iris")rx_data_step(input_data = df, output_file = table_ref, overwrite = True)print("New Table Created: Iris")

print("Sklearn Iris sample loaded into Iris table")

Define a Function to Send to SQL Server

Write any python code you want to execute in SQL. In this example we are creating a scatter matrix on the iris dataset and only returning the bytestream of the .png back to Jupyter Notebooks to render on our client.

def send_this_func_to_sql():

from revoscalepy import RxSqlServerData, rx_import

from pandas.tools.plotting import scatter_matrix

import matplotlib.pyplot as plt

import io

# remember the scope of the variables in this func are within our SQL Server Python Runtime

connection_string = "Driver=SQL Server;Server=localhost\MSSQLSERVER2017; Database=MLRemoteExec;Trusted_Connection=Yes;"

# specify a query and load into pandas dataframe df

sql_query = RxSqlServerData(connection_string=connection_string, sql_query = "select * from Iris")

df = rx_import(sql_query)

scatter_matrix(df)

# return bytestream of image created by scatter_matrix

buf = io.BytesIO()

plt.savefig(buf, format="png")

buf.seek(0)

return buf.getvalue()

Send execution to SQL

Now that we are finally set up, check out how easy sending remote execution really is! First, import revoscalepy. Create a sql_compute_context, and then send the execution of any function seamlessly to SQL Server with RxExec. No raw data had to be transferred from SQL to the Jupyter Notebook. All computation happened within the database and only the image file was returned to be displayed.

from IPython import display

import matplotlib.pyplot as plt

from revoscalepy import RxInSqlServer, rx_exec# create a remote compute context with connection to SQL Server

sql_compute_context = RxInSqlServer(connection_string=connection_string.format(new_db_name))

# use rx_exec to send the function execution to SQL Server

image = rx_exec(send_this_func_to_sql, compute_context=sql_compute_context)[0]

# only an image was returned to my jupyter client. All data remained secure and was manipulated in my db.

display.Image(data=image)

While this example is trivial with the Iris dataset, imagine the additional scale, performance, and security capabilities that you now unlocked. You can use any of the latest open source R/Python packages to build Deep Learning and AI applications on large amounts of data in SQL Server. We also offer leading edge, high-performance algorithms in Microsoft’s RevoScaleR and RevoScalePy APIs. Using these with the latest innovations in the open source world allows you to bring unparalleled selection, performance, and scale to your applications.

Learn More

Check out SQL Machine Learning Services Documentation to learn how you can easily deploy your R/Python code with SQL stored procedures making them accessible in your ETL processes or to any application. Train and store machine learning models in your database bringing intelligence to where your data lives.

Basic R and Python Execution in SQL Server: https://aka.ms/BasicMLServicesExecution
Set up Machine Learning Services in SQL Server: https://aka.ms/SetupMLServices
End-to-end tutorial solutions on Github: https://microsoft.github.io/sql-ml-tutorials/

Interview – Über die Kunst, Daten als Produktionsfaktor zu erkennen

August 8, 2018/0 Comments/in Insights, Interview mit CIO, Interviews, Projectmanagement /by Benjamin Aunkofer

Interview mit Dr. Christina Bender über die Digitalisierung und Data Science in einem 270-jährigem Familienunternehmen.

Dr. Christina Bender ist Senior Digital Strategist mit Schwerpunkt auf Data Science bei der Villeroy & Boch AG. Sie ist Diplom-Finanzökonomin und promovierte Mathematikerin. Als „Quant“ bei der UniCredit und Unternehmensberaterin bei der d‑fine GmbH sammelte sie bereits langjährige Erfahrung in der Konzeption und Umsetzung interdisziplinärer Digitalisierungs- und Prozessthemen in diversen Branchen. Als letzte Herausforderung im „echten“ Beraterleben hat sie bei d-fine als Prokuristin den Geschäftsbereich „Digitalisierung im Gesundheitswesen“ mit aufgebaut.

In der Digital Unit bei V&B bündelt sie als eine Art interne Beraterin alle Aktivitäten rund um Data Science (interimsweise inklusive Process Digitisation) für den Gesamtkonzern von Produktion über SCM bis CRM und Sales von der Strategie bis zur Betreuung der Umsetzung. Als Gründungsmitglied der Digital Unit hat sie die neue Unit und die digitale Roadmap von V&B aktiv gestaltet.

In ihrer beruflichen Karriere spielten komplexe Zusammenhänge und Daten also schon früh eine Rolle. Durch ihr breites Erfahrungsspektrum hat sie gelernt, dass Daten erst zum Produktionsfaktor werden, wenn sie in Anwendungsgebieten richtig angepasst eingesetzt und überzeugend präsentiert werden.

Data Science Blog: Frau Dr. Bender, womit genau befassen Sie sich als Digital Strategist? Und wie passt Data Science in dieses Konzept?

Zunächst war es die Aufgabe eine digitale Roadmap zu entwickeln und zwar abgestimmt auf ein Traditionsunternehmen, das sich in den letzten 270 Jahren ständig durch Innovation verändert hat. Als Beispiel, V&B hatte einen erfolgreichen „Merger“ vollzogen, da gab es das Wort „M&A“ noch gar nicht.

Ein erster Schritt war es dabei Themen zu sammeln und ein Vorgehen zu entwickeln, diese zu verstehen, zu priorisieren und sie dann stets als Ziel im Blick umzusetzen. Die meisten der Themen haben immer mit Daten und damit häufig mit Data Science zu tun. Das geht von Fragestellungen z.B. im Vertrieb, die durch einen Bericht im ERP-System abbildbar sind, bis hin zu komplexen Fragen der Bilderkennungstechnologie in der Produktion oder im Customer Relationship Management.

Um weiterhin die wirklich wichtigen Themen zu finden, ist es entscheidend die Chancen und Risiken der Digitalisierung und den Wert der richtigen Daten weit in die Fläche des Unternehmens zu tragen. Dieser Aufbau interner Kompetenzen durch uns als Digital Unit schafft Vertrauen und ist neben dem Vorantreiben konkreter Anwendungsfälle essentieller Bestandteil für eine erfolgreiche Digitalisierung.

Data Science Blog: An was für Anwendungsfällen arbeiten Sie konkret? Und wohin geht die Reise langfristig?

Derzeit arbeiten wir sowohl an kleineren Fragestellungen als auch an ca. vier größeren Projekten. Letztere sollen pain points gemeinsam mit den Fachexperten lösen und dadurch zu Leuchtturmprojekten werden, um eben Vertrauen zu schaffen. Dafür müssen wir ein “Henne-Ei”-Problem lösen. Oft sind die richtigen Daten für die Fragestellung noch nicht erfasst und/oder einige Menschen involviert, die eben erst durch ihnen nahestehende Leuchtturmprojekte überzeugt werden müssten. Daher arbeiten wir für eine erfolgreiche Umsetzung mit im täglichen Geschäft involvierten Fachexperten und erfahrenen Data Scientists mit gewissem Fach-Know-How, die uns einen gewissen Vertrauensvorsprung geben.

Das dauert seine Zeit, insbesondere weil wir stark agil vorgehen, um uns nicht zu verheddern. D.h. oft sieht eine Fragestellung am Anfang leicht aus und ist dann schlicht weg nicht realisierbar. Das muss man dann akzeptieren und eben auf die nächst priorisierte Fragestellung setzen. “Keramik ist halt anders als die Autoindustrie.” Über genaue Use Cases möchte ich daher noch nicht sprechen. Wir sind auf einem guten Weg.

Langfristig wünsche ich mir persönlich, dass Werte aus Daten – insbesondere bessere Entscheidungen durch Wissen aus Daten – möglichst selbständig durch Business-Experten geschaffen werden und dies durch ein schlagkräftiges zentrales Team ermöglicht wird. D.h. das Team sorgt für eine entsprechende stets aktuell für Data Science geeignete Infrastruktur und steht bei komplexen Fragestellungen zur Verfügung.

Data Science Blog: Welche Algorithmen und Tools verwenden Sie für Ihre Anwendungsfälle?

Wir arbeiten auch mit Methoden im Bereich „Deep Learning“, zum Beispiel für die Bilderkennung. Allerdings gerade um die Erwartungshaltung im Unternehmen nicht zu hoch zu hängen, schauen wir immer wofür sich diese Methodik eignet und wo sie nicht unsere eigentliche Frage beantworten kann (siehe unten) oder schlicht weg nicht genügend Daten verfügbar sind. Insbesondere, wenn wir die eigentlich Ursache eines Problems finden und darauf reagieren wollen, ist es schlecht, wenn sich die Ursache „tief“ im Algorithmus versteckt. Dafür eignet sich z.B. eine logistische Regression, sofern gut parametrisiert und mit gut aufbereiteten Daten befüttert, häufig deutlich besser.

Wir nutzen kostenpflichtige Software und Open Source. Wunsch wäre, möglichst jedem im Unternehmen die richtige Anwendung zur Verfügung zu stellen, damit sie oder er leicht selbst die richtige Exploration erstellen kann, um die richtige Entscheidung zu treffen. Für den Data Scientist mag das ein anderes Tool sein als für den Fachexperten im Geschäftsbereich.

Data Science Blog: Daten werden von vielen Unternehmen, vermutlich gerade von traditionsreichen Familienunternehmen, hinsichtlich ihres Wertes unterschätzt. Wie könnten solche Unternehmen Daten besser bewerten?

Unternehmen müssen sich genau überlegen, was die für sie richtigen Fragen sind. Aus welchen Daten oder deren Verknüpfung kann ich Wissen generieren, dass diese für mich relevante Fragen (überhaupt) beantwortet werden können, um mit vertretbarem Aufwand nachhaltig Mehrwerte zu generieren. Natürlich sind die schlimmsten „pain points“ immer am schwierigsten, sonst hätte sie vermutlich jemand vor mir gelöst. Dies wird stets begleitet, warum mit den schon gesammelten Daten noch kein Mehrwert generiert wurde und somit ggf. begründet warum kein (Zeit-)Budget frei gegeben wird, um weitere (dann hoffentlich die richtigen) Daten zu sammeln.

Als erstes ist es m.E. daher wichtig dem Entscheidungsträger klar zu machen, dass es keine Maschine gibt in die ggf. wahllos gesammelte Daten reingeworfen werden und die „KI“ spuckt dann die richtigen Antworten auf die richtigen nie gestellten Fragen heraus. Denn gäbe es diese Art künstlicher Intelligenz, wäre der Erfinder wohl längst der reichste Mensch der Welt.

Nein, dafür wird menschliche Intelligenz gebraucht und Freiraum für die Mitarbeiterinnen und Mitarbeiter, die richtigen Fragen und Antworten zu suchen und auch auf diesem Weg manchmal kurzfristig zu scheitern. Kurz gesagt, braucht es eine Datenstrategie, um alle, Vorstand und Mitarbeiterinnen und Mitarbeiter, auf diesen Weg mitzunehmen.

Data Science Blog: Wie erstellen Unternehmen eine Datenstrategie?

Unternehmensleiter wollen Ergebnisse sehen und verstehen oft nicht gleich, warum sie Geld in Daten investieren sollen, wenn erst mittel- bis langfristig ein Mehrwert herausspringt. Die alleinige Drohkulisse, wenn nicht jetzt, dann eben in 10 Jahren ohne uns, hilft da oft nur bedingt oder ist gar kontraproduktiv.

Wichtig ist es daher, alle an einen Tisch zu holen und gemeinsam eine Unternehmensvision und Ziele zu diskutieren, zu begreifen und zu vereinbaren, dass Daten dafür ein Faktor sind (oder ggf. vorerst auch nicht). Noch wichtiger ist der Weg dahin, die Datenstrategie, nämlich wie aus Daten langfristig nachhaltige Mehrwerte gehoben werden.

Um eine Datenstrategie zu erstellen, braucht es eine gewisse Mindestausstattung einerseits an dafür zumindest zum Teil freigestellten Experten aus dem Business und anderseits Datenexperten, die mit diesen Experten reden können. Sie müssen nach erfolgreicher Zielbildung einen minimalen Werkzeugkasten aus KnowHow und Technologie schaffen, der es erst ermöglicht Leuchtturmprojekte erfolgreich umzusetzen. Diese Leuchtturmprojekte dienen als erste erfolgreiche Beispielwege. Damit fällt es auch leichter den Werkzeugkasten als Grundlage zur Lösung größerer pain points weiter auszubauen. In Zeiten, wo halbwegs kommunikative Data Scientists mit Businessverständnis Mangelware sind, ist dies manchmal nur mit externer Unterstützung möglich. Doch Obacht, wichtig ist ein interner Koordinator, der alle Zügel in Händen behält, damit nicht viele richtige Antworten auf irrelevante nicht gestellte Fragen gegeben werden. Denn dann geht anfängliche Akzeptanz leicht verloren.

Data Science Blog: Wie stellen Sie ein Data Science Team auf? Und suchen Sie für dieses Team eher Nerds oder extrovertierte Beratertypen?

Kurz und knapp: Die gesunde Mischung wie ich selbst.

Natürlich ist je nach Aufgabengebiet die Gewichtung etwas verschoben. Gerade in einem Unternehmen, das gerade erst den Wert von Daten am entdecken ist, ist es entscheidend, dass diese Werte den Businessexperten auch begreiflich gemacht bzw. mehr noch zusammen entwickelt werden. Dafür brauchen wir Menschen, die beides beherrschen. D.h. sie können komplizierte Inhalte anschaulich vermitteln – „Anteil extrovertierter Berater“, und hinter den Kulissen den tatsächlichen Wert aus Daten finden. Für letzteres brauchen wir die Eigenschaften eines „Nerds“. Mal ehrlich, durch meine Lehrtätigkeit habe ich selbst gelernt: Erst wenn ich etwas selbst verständlich erklären kann, habe ich es selbst verstanden und kann mein Tun stetig verbessern.

Dr. Christina Bender präsentiert am 15. November 2018, dem zweiten Tag der Data Leader Days 2018, über die „Tradition und digitale Innovation bei einem Keramikhersteller – warum Deep Learning nicht immer das Allheilmittel ist“. Mehr über die Data Leader Days erfahren Sie hier: www.dataleaderdays.com

Interview – Berufsbegleitender Zertifikatskurs “Data Science”

August 2, 2018/0 Comments/in Certification / Training, Education / Certification, Interviews /by Benjamin Aunkofer

Interview mit Dr. Peter Lauf, dem wissenschaftlichen Leiter des berufsbegleitenden Zertifikatskurses „Data Science“ der Technischen Hochschule Brandenburg, über die Erfahrungen aus bisher drei erfolgreichen Zertifikatskursen.

Dr. Peter Lauf studierte im Anschluss an eine kaufmännische Ausbildung Volkswirtschaft. Sein Diplom und die Promotion machte er an der Uni Köln. Heute ist er vor allem als Datenanalytiker, Marketing Manager, Management Consultant, Leiter Database und Manager Big Data tätig. Er verfügt über mehr als 20 Jahre Erfahrung mit SPSS, ist zertifizierter SAS‑Programmierer und nutzt die Programmiersprache R seit 2004. Neben seinen Tätigkeiten als Consultant für Daten, steht er in Lehraufträgne an verschiedenen Hochschulen.

Data Science Blog: Vor welchem Hintergrund haben Sie das Curriculum für die Weiterbildung zum Data Scientist entwickelt?

Maßgeblich waren hier zunächst eigene, über Jahrzehnte hinweg gesammelte Erfahrungen. Ich arbeitete unter anderem als Sozialforscher, Datenbankmanager, Management Consultant und Manager Big Data in den unterschiedlichsten Branchen mit den unterschiedlichsten Technologien. Weil ich bis heute parallel an verschiedenen Hochschulen tätig bin, besitze ich auch einen guten Überblick über aktuelle Webseiten, Blogs und Publikationen.

Data Science Blog: Wie setzen sie diese Erfahrungen und dieses Wissen konkret um?
Durch konsequenten Praxisbezug. Ein Beispiel: In der Praxis besitzt Excel für die Datenvorbereitung eine überragende Rolle. Da werden dann Inputdateien in verformelten Arbeitsblättern vielfach hin und her kopiert. Derartige Lösungen bedingen einen hohen manuellen Aufwand, sind praktisch nicht dokumentierbar und führen zu einer hohen Abhängigkeit von einzelnen Mitarbeitern. Weil ich selbst an der Ablösung solcher Systeme durch ETL-Lösungen mitgearbeitet habe, kann ich den Übergang von der einen zur anderen Lösung und die damit verbundenen Vorteile praxisnah und überzeugend darstellen.

Data Science Blog: Wie kommunizieren Sie mit den Teilnehmern?
Auf durchaus vielfältige Weise. In den Präsenzen spielt das direkte Gespräch eine große Rolle und zwar sowohl in den Unterrichtseinheiten, wie auch im Off, den Kaffeepausen zum Beispiel. Ein offenes Ohr bildet eine Grundvoraussetzung für einen guten Kurs. In den Web-Konferenzen werden ebenfalls Fragen gestellt und beantwortet. Mit Moodle verfügen wir auch über eine leistungsfähige und gern genutzte Lern- und Kommunikationsplattform. Schließlich unterstützen wir aktiv die Bildung einer Community unter den Teilnehmern. Es ist erstaunlich, wieviel Teilnehmer (und Dozenten!) aus diesem Austausch lernen können.

Data Science Blog: Lassen Sie uns hier einhaken, was lernen Sie von den Teilnehmern?

Bisher streut der Kurs ganz erheblich bezüglich Branchen, Alter, Vorerfahrungen, Job-Titles und anderer Kriterien. Diese Diversität konfrontiert uns immer wieder mit neuen Anwendungsfällen, die wir gerne aufgreifen und für die wir Lösungen zur Diskussion stellen. Es ist wie in der Medizin: ein breites Fallspektrum steigert die Qualität.

Data Science Blog: Welche Pläne haben Sie für die Zukunft?

Die dynamische Weiterentwicklung unserer Inhalte. Wir betreiben einen hohen Aufwand um á jour zu bleiben. Die Aktivitäten international führender Data Scientists werden aufmerksam verfolgt und wir werten z. B. Verlagsprogramme und Konferenzen aus. Soweit neue Entwicklungen bereits in Software umgesetzt wurden und für uns interessant sind, testen wir diese Lösungen und integrieren sie in unsere Lernprogramme. Abgesehen von der reinen Datenseite sehen wir einen zukünftigen Schwerpunkt in der Berücksichtigung der Kognitionswissenschaft mit dem Ziel, die Urteilskraft unserer Teilnehmer weiter zu stärken.

Dr. Peter Lauf ist wissenschaftlicher Leiter des berufsbegleitenden Zertifikatskurses „Data Science“, der von der Agentur für wissenschaftliche Weiterbildung und Wissenstransfer (AWW e. V.) an der Technischen Hochschule Brandenburg angeboten wird. Die Module sind als eigene Einheiten konzipiert, so dass ein Einsteigen in den Kurs mit jedem Modul möglich ist. Weitere Hinweise zu diesem Fortbildungsangebot finden sich direkt auf www.aww-brandenburg.de.