December 2017 – Data Science Blog

Maschinelles Lernen: Klassifikation vs Regression

December 20, 2017/6 Comments/in Artificial Intelligence, Business Analytics, Data Mining, Data Science, Deep Learning, Machine Learning, Main Category, Mathematics, Predictive Analytics /by Benjamin Aunkofer

Das ist Artikel 2 von 4 aus der Artikelserie – Was ist eigentlich Machine Learning? Die Unterscheidung zwischen Klassifikation und Regression ist ein wichtiger Schritt für das Verständnis von Predictive Analytics. Nun möchte ich eine Erklärung liefern, die den Unterschied (hoffentlich) deutlich macht.

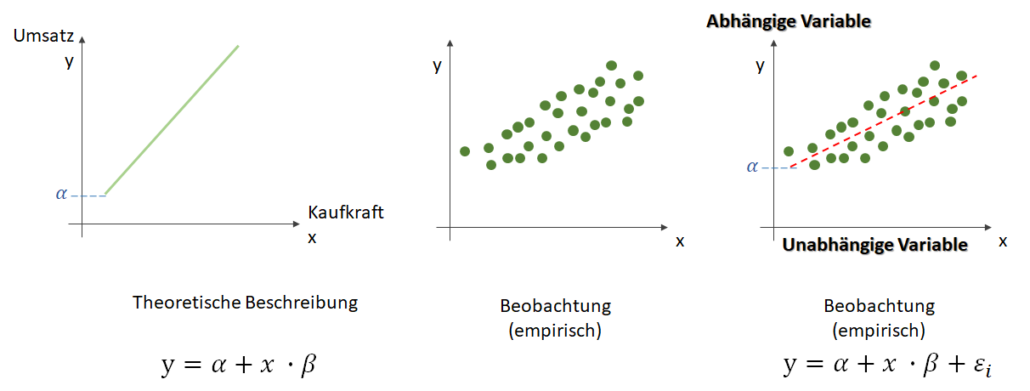
Regression – Die Vorhersage von stetigen Werten

Wir suchen bei der Regression demnach eine Funktion $y = \beta \cdot x + \alpha$ , die unsere Punktwolke – mit der wir uns zutrauen, Vorhersagen über die abhängige Variable vornehmen zu können – möglichst gut beschreibt. Dabei ist $y$ der Zielwert (abhängige Variable) und $x$ der Eingabewert. Wir arbeiten also in einer zwei-dimensionalen Welt. Variablen, die die Funktion mathematisch definieren, werden oft als griechische Buchstaben darsgestellt. Die Variable $\alpha$ (Alpha) ist der $y$ -Achsenschnitt bei $x = 0$ . Dieser wird als Bias, selten auch als Default-Wert, bezeichnet. Der Bias ist also der Wert, wenn die $x$ -Eingabe gleich Null ist. Eine weitere Variable $\beta$ (Beta) beschreibt die Steigung.

Ferner ist zu beachten, dass sich eine Punktwolke durch eine Gerade nie perfekt beschreiben lässt, und daher für jedes $x_{i}$ ein Fehler $\varepsilon_{i}$ existiert. Diesen Fehler wollen wir in diesem Artikel ignorieren.

In einem zwei-dimensionalen System (eine Eingabe und eine Ausgabe) sprechen wir von einer einfachen Regression. Generalisieren wir die Regressionsmethode auf ein multivariates System (mehr als eine Eingabe-Variable), werden die Variablen in der Regel nicht mehr als griechische Buchstaben (denn auch das griechische Alphabet ist endlich) dargestellt, sondern wir nehmen eines abstrahierende Darstellung über Gewichtungen (weights). Dies ist eine sehr treffende Symbolisierungen, denn sowohl der Bias ( $w_{0}$ statt $\alpha$ ) als auch die Steigungen ( $w_{1\ldots n}$ ) sind nichts anderes als Gewichtungen zwischen den Eingaben.

$y = w_{0} \cdot x_{0} + w_{1} \cdot x_{1} + \ldots + w_{n} \cdot x_{n}$

$y$ ist eine Summe aus den jeweiligen Produkten aus $x_{i}$ und $w_{i}$ . Verkürzt ausgedrückt:

$y = \sum_{i=0}^n w_{i} \cdot x_{i}$

Noch kürzer ausgedrückt:

$y = w^T \cdot x$

Anmerkung: Das hochgestellte T steht für Transponieren, eine Notation aus der linearen Algebra, die im Ergebnis nichts anderes bewirkt als $y = \sum_{i=0}^n w_{i} \cdot x_{i}$ .

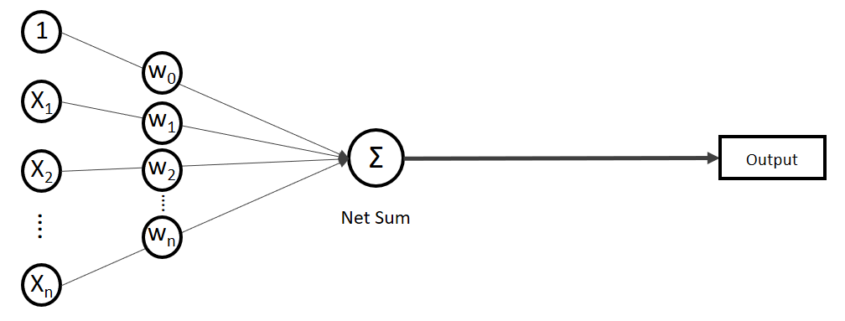
Diese mathematische lineare Funktion kann wie folgt abgebildet werden:

Der Output ist gleich $y$ bzw. die Ausgabe der Nettoeingabe (Net Sum) $w^T \cdot x$ . Auf der linken Seite finden wir alle Eingabewerte, wobei der erste Wert statisch mit 1.0 belegt ist, nur für den Zweck, den Bias ( $w_{0}$ ) in der Nettoeingabe aufrecht zu erhalten. Im Falle einer einfachen linearen Regression hätten wir also eine Funktion mit zwei Gewichten: $y = 1 \cdot w_{0} + x \cdot w_{1}$

Das Modell beschreibt, wie aus einer Reihe von Eingabewerten (n = Anzahl an x-Dimensionen) und einer Reihe von Gewichtungen (n + 1) eine Funktion entsteht, die einen y-Wert berechnet. Diese Berechnung wird auch als Forward-Propagation bezeichnet.
Doch welche Werte brauchen wir für die Gewichtungen, damit bei gegebenen x-Werten ein (mehr oder weniger) korrekter y-Wert berechnet wird? Anders gefragt, wie schaffen wir es, dass die Forward-Propagation die richtigen Werte ausspuckt?

Mit einem Training via Backpropagation!

Einfache Erklärung der Backpropagation

Die Backpropagation ist ein Optimierungsverfahren, unter Einsatz der Gradientenmethode, den Fehler einer Forward-Propagation zu berechnen und die Gewichtungen in Gegenrichtung des Fehlers anzupassen. Optimiert wird in der Form, dass der Fehler minimiert wird. Es ist ein iteratives Verfahren, bei dem mit jedem Iterationsschritt wieder eine Forward-Propagation auf Basis von Trainingsdaten durchgeführt wird und die Prädiktionsergebnisse mit den vorgegebenen Ergebnissen (der gekennzeichneten Trainingsdaten) verglichen und damit die Fehler berechnet werden. Die resultierende Fehlerfunktion ist konvex, ableitbar und hat ein zentrales globales Minimum. Dieses Minimum finden wir durch diese iterative Vorgehensweise.

Die Backpropagation zu erklären, erfordert einen separaten Artikel. Merken wir uns einfach: Die Backpropagation nutzt eine Fehlerfunktion, um die Werte der Gewichtungen schrittweise entgegen des Fehlers (bei jeder Forward-Propagation) bis zu einem Punkt anzupassen, bis keine wesentliche Verbesserung (Reduzierung des Fehlers) mehr eintritt. Nach dem Vollzug der Backpropagation erhalten wir die “richtigen” Gewichtungen und haben eine Funktion zur Vorhersage von y-Werten bei Eingabe neuer x-Werte.

Klassifikation – Die Vorhersage von Gruppenzugehörigkeiten

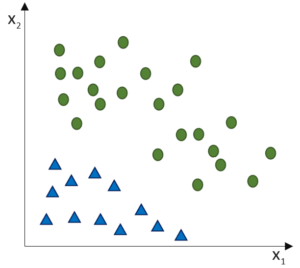
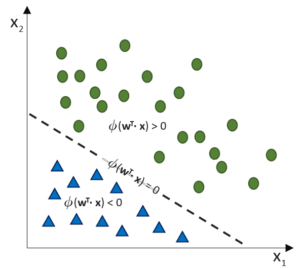
Bei der Klassifikation möchten wir jedoch keine Gerade oder Kurve vorhersagen, die sich durch eine Punktwolke legt, sondern wie möchten Punktwolken voneinander als Klassen unterscheiden, um später hinzukommende Punkte ihren richtigen Klassen zuweisen zu können (Klassifikation). Wir können jedoch auf dem vorherigen Modell der Prädiktion von stetigen Werten aufbauen und auch die Backpropagation zum Training einsetzen, möchten das Training dann jedoch auf die Trennung der Punktwolken ausrichten.

Hinweis: Regressions- und Klassifikationsherausforderungen werden in den Dimensionen unterschiedlich dargestellt. Zur Veranschaulichung: Während wir bei der einfachen Regression eine x-Eingabe als unabhängige Variable und eine y-Ausgabe als abhängige Variable haben, haben wir bei einer zwei-dimensionalen Klassifikation zwei x-Dimensionen als Eingabe. Die Klassen sind die y-Ausgabe (hier als Farben visualisiert).

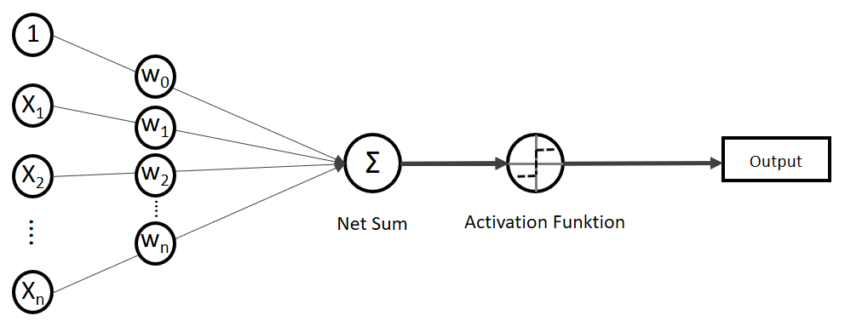
Ergänzen wir das Modell nun um eine Aktivierungsfunktion, dass die stetigen Werte der Nettosumme über eine Funktion in Klassen unterteilt, erhalten wir einen Klassifikator: Den Perceptron-Klassifikator. Das Perzeptron gilt als der einfachste Klassifikator und ist bereits die kleinste Form eines künstlichen neuronalen Netzes. Es funktioniert nur bei linearer Trennbarkeit der Klassen.

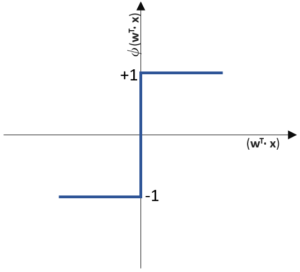
Was soll die Aktivierungsfunktion bewirken? Wir berechnen wieder eine Nettoeingabe $w^T \cdot x$ , die uns stetige Werte ausgiebt. Wir haben also immer noch unsere Gewichtungen, die wir trainieren können. Nun trainieren wir nur nicht auf eine “korrekte” stetige Ausgabe der Nettoeingabe hin, sondern auf eine korrekte Ausgabe der Aktivierungsfunktion $\phi$ (Phi), die uns die stetigen Werte der Nettoeingabe in einen binären Wert (z. B. 0 oder 1) umwandelt. Das Perzeptron ist die kleinste Form des künstlichen neuronalen Netzes und funktioniert wie der lineare Regressor, jedoch ergänzt um eine Aktivierungsfunktion die bewirken soll, dass ein Neuron (hier: der einzelne Output) “feuert” oder nicht “feuert”. Es ist ein binärer Klassifikator, der beispielsweise die Wertebereiche -1 oder +1 annehmen kann.

Das Perceptron verwendet die einfachste Form der Aktivierungsfunktion: Eine Sprungfunktion, die einer einfachen if… else… Anweisung gleich kommt.

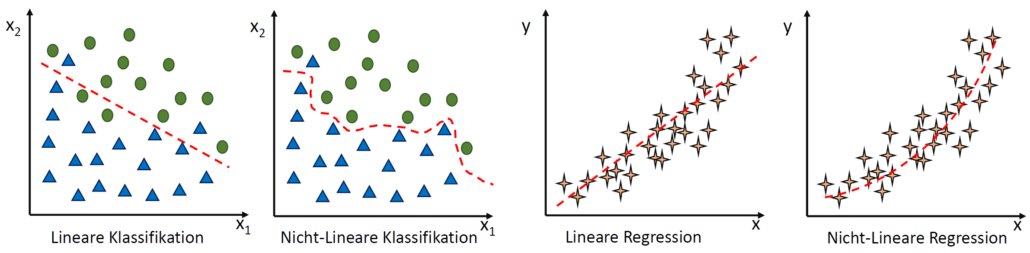
$y = \phi(w^T \cdot x) = \left\{ \begin{array}{12} 1 & w^T \cdot x > 0\\ -1 & \text{otherwise} \end{array}$

Fazit – Unterschied zwischen Klassifikation und Regression

Mathematisch müssen sich Regression und Klassifikation gar nicht all zu sehr voneinander unterscheiden. Viele Verfahren der Klassifikation lassen sich mit nur wenig Anpassung auch zur Regression anwenden, oder umgekehrt. Künstliche neuronale Netze, k-nächste-Nachbarn und Entscheidungsbäume sind gute Beispiele, die in der Praxis sowohl für Klassifkation als auch für Regression eingesetzt werden, natürlich mit unterschiedlichen Stärken und Schwächen.

Unterschiedlich ist jedoch der Zweck der Anwendung: Bei der Regression möchten wir stetige Werte vorhersagen (z. B. Temperatur der Maschine), bei der Klassifikation hingegen Klassen unterscheiden (z. B. Maschine überhitzt oder überhitzt nicht).

Unterschiede zwischen linearer und nicht-linearer Klassifikation und linearer und nicht-linearer Regression. Für Einsteiger in diese Thematik ist beachten, dass jede maschinell erlernte Klassifikation und Regression einen gewissen Fehler hat, der unter Betrachtung der Trainings- und Testdaten zu minimieren ist, jedoch nie ganz verschwindet.

Und Clustering?

Clustering ist eine Disziplin des unüberwachten Lernens, um Gruppen von Klassen bzw. Grenzen dieser Klassen innerhalb von unbekannten Daten zu finden. Es ist im Prinzip eine untrainierte Klassifikation zum Zwecke des Data Minings. Clustering gehört auch zum maschinellen Lernen, ist aber kein Predictive Analytics. Da keine – mit dem gewünschten Ergebnis vorliegende – Trainingsdaten vorliegen, kann auch kein Training über eine Backpropagation erfolgen. Clustering ist folglich eine schwache Klassifikation, die mit den trainingsbasierten Klassifikationsverfahren nicht funktioniert.

Process Analytics – Data Analysis for Process Audit & Improvement

December 14, 2017/1 Comment/in Audit Analytics, Business Analytics, Business Intelligence, Data Mining, Data Science, Insights, Main Category, Process Mining /by Benjamin Aunkofer

Process Mining: Innovative data analysis for process optimization and audit

Step-by-Step: New ways to detect compliance violations with Process Analytics

In the course of the advancing digitization, an enormous upheaval of everyday work is currently taking place to ensure the complete recording of all steps in IT systems. In addition, companies are increasingly confronted with increasingly demanding regulatory requirements on their IT systems.

Read this article in German:
“Process Mining: Innovative Analyse von Datenspuren für Audit und Forensik “

The unstoppable trend towards a connected world will further increase the possibilities of process transparency, but many processes in the company area are already covered by one or more IT systems. Each employee, as well as any automated process, leaves many data traces in IT backend systems, from which processes can be replicated retroactively or in real time. These include both obvious processes, such as the entry of a recorded purchase order or invoice, as well as partially hidden processes, such as the modification of certain entries or deletion of these business objects.

1 Understanding Process Analytics

Process Analytics is a data-driven methodology of the actual process analysis, which originates in forensics. In the wake of the increasing importance of computer crime, it became necessary to identify and analyze the data traces that potential criminals left behind in IT systems in order to reconstruct the event as much as possible.

With the trend towards Big Data Analytics, Process Analytics has not only received new data bases, but has also been further developed as an analytical method. In addition, the visualization enables the analyst or the report recipient to have a deeper understanding of even more complex business processes.

While conventional process analysis primarily involves employee interviews and monitoring of the employees at the desk in order to determine actual processes, Process Analytics is a leading method, which is purely fact-based and thus objectively approaching the processes. It is not the employees who are asked, but the IT systems, which not only store all the business objects recorded in a table-oriented manner, but also all process activities. Every IT system for enterprise purposes log all relevant activities of the whole business process, in the background and invisible to the users, such as orders, invoices or customer orders, with a time stamp.

2 The right choice of the processes to analyze

Today almost every company works with at least one ERP system. As other systems are often used, it is clear which processes can not be analyzed: Those processes, which are still carried out exclusively on paper and in the minds of the employees, which are typical decision-making processes at the strategic level and not logged in IT systems.

Operational processes, however, are generally recorded almost seamlessly in IT systems. Furthermore, almost all operational decisions are recorded by status flags in datasets.

The operational processes, which can be reconstructed and analyzed with Process Mining very well and which are of equal interest from the point of view of compliance, include for example:

– Procurement

– Logistics / Transport

– Sales / Ordering

– Warranty / Claim Management

– Human Resource Management

Process Analytics enables the greatest possible transparency across all business processes, regardless of the sector and the department. Typical case IDs are, for example, sales order number, procurement order number, customer or material numbers.

3 Selection of relevant IT systems

In principle, every IT system used in the company should be examined with regard to the relevance for the process to be analyzed. As a rule, only the ERP system (SAP ERP or others) is relevant for the analysis of the purchasing processes. However, for other process areas there might be other IT systems interesting too, for example separate accounting systems, a CRM or a MES system, which must then also be included.

Occasionally, external data should also be integrated if they provide important process information from externally stored data sources – for example, data from logistics partners.

4 Data Preparation

Before the start of the data-driven process analysis, the data directly or indirectly indicating process activities must be identified, extracted and processed in the data sources. The data are stored in database tables and server logs and are collected via a data warehousing procedure and converted into a process protocol or – also called – event log.

The event log is usually a very large and wide table which, in addition to the actual process activities, also contains parameters which can be used to filter cases and activities. The benefit of this filter option is, for example, to show only process flows where special product groups, prices, quantities, volumes, departments or employee groups are involved.

5 Analysis Execution

The actual inspection is done visually and thus intuitively with an interactive process flow diagram, which represents the actual processes as they could be extracted from the IT systems. The event log generated by the data preparation is loaded into a data visualization software (e.g. Celonis PM Software), which displays this log by using the case IDs and time stamps and transforms this information in a graphical process network. The process flows are therefore not modeled by human “process thinkers”, as is the case with the target processes, but show the real process flows given by the IT systems. Process Mining means, that our enterprise databases “talk” about their view of the process.

The process flows are visualized and statistically evaluated so that concrete statements can be made about the process performance and risk estimations relevant to compliance.

6 Deviation from target processes

The possibility of intuitive filtering of the process presentation also enables an analysis of all deviation of our real process from the desired target process sequences.

The deviation of the actual processes from the target processes is usually underestimated even by IT-affine managers – with Process Analytics all deviations and the general process complexity can now be investigated.

6 Detection of process control violations

The implementation of process controls is an integral part of a professional internal control system (ICS), but the actual observance of these controls is often not proven. Process Analytics allows circumventing the dual control principle or the detection of functional separation conflicts. In addition, the deliberate removal of internal control mechanisms by executives or the incorrect configuration of the IT systems are clearly visible.

7 Detection of previously unknown behavioral patterns

After checking compliance with existing controls, Process Analytics continues to be used to recognize previously unknown patterns in process networks, which point to risks or even concrete fraud cases and are not detected by any control due to their previously unknown nature. In particular, the complexity of everyday process interlacing, which is often underestimated as already mentioned, only reveals fraud scenarios that would previously not have been conceivable.

8 Reporting – also possible in real time

As a highly effective audit analysis, Process Analytics is already an iterative test at intervals of three to twelve months. After the initial implementation, compliance violations, weak or even ineffective controls, and even cases of fraud, are detected reliably. The findings can be used in the aftermath to stop the weaknesses. A further implementation of the analysis after a waiting period makes it possible to assess the effectiveness of the measures taken.

In some application scenarios, the seamless integration of the process analysis with the visual dashboard to the IT system landscape is recommended so that processes can be monitored in near real-time. This connection can also be supplemented by notification systems, so that decision makers and auditors are automatically informed about the latest process bottlenecks or violations via SMS or e-mail.

Fazit

Process Analytics is, in the course of the digitalization, the highly effective methodology from the area of Big Data Analysis for detecting compliance-relevant events throughout the company and also providing visual support for forensic data analysis. Since this is a method, and not a software, an expansion of the IT system landscape, especially for entry, is not absolutely necessary, but can be carried out by internal or external employees at regular intervals.

Neues Weiterbildungsangebot zu Programmiersprache R an der TU Dortmund

December 12, 2017/in Certification / Training, Data Science News, Education / Certification /by Redaktion

Anzeige: Neues Weiterbildungsangebot zu Programmiersprache R an der TU Dortmund

In der Tagesseminarreihe „Dortmunder R-Kurse“ an der Technischen Universität Dortmund vermitteln erfahrene Experten die praktische Anwendung der Open-Source Statistiksoftware R. Die Teilnehmenden erwerben dadurch Schlüsselkompetenzen im Umgang mit Big Data.

Das Seminar R-Basiskurs für Anfänger findet am 22.02. & 23.02.18 statt. Den Teilnehmern wird der praxisrelevante Part der Programmiersprache näher gebracht, um so die Grundlagen zur ersten Datenanalyse — vom Datensatz zu statistischen Kennzahlen und ersten Datenvisualisierungen — zu schaffen. Anmeldeschluss ist der 01.02.2018.

Das Seminar R-Vertiefungskurs für Fortgeschrittene findet am 06.03. & 07.03.18 statt. Die Veranstaltung ist ideal für Teilnehmende mit ersten Vorkenntnissen, die ihre Analysen effizient mit R durchführen möchten. Anmeldeschluss ist der 13.02.2018.

Weitere inhaltliche Informationen zu den R-Kursen finden Sie unter:
http://dortmunder-r-kurse.de/

ID3-Algorithmus: Ein Rechenbeispiel

December 8, 2017/4 Comments/in Artificial Intelligence, Business Analytics, Customer Analytics, Data Mining, Data Science, Machine Learning, Main Category, Predictive Analytics, Statistics, Visualization /by Benjamin Aunkofer

Dieser Artikel ist Teil 3 von 4 der Artikelserie Maschinelles Lernen mit Entscheidungsbaumverfahren und nun wollen wir einen Entscheidungsbaum aus Daten herleiten, jedoch ohne Programmierung, sondern direkt auf Papier (bzw. HTML :-).

Folgender Datensatz sei gegeben:

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
1	Neukunde	niedrig	niedrig	Inland	false
2	Neukunde	niedrig	niedrig	Ausland	false
3	Stammkunde	niedrig	niedrig	Inland	true
4	Normalkunde	mittel	niedrig	Inland	true
5	Normalkunde	hoch	hoch	Inland	true
6	Normalkunde	hoch	hoch	Ausland	false
7	Stammkunde	hoch	hoch	Ausland	true
8	Neukunde	mittel	niedrig	Inland	false
9	Neukunde	hoch	hoch	Inland	true
10	Normalkunde	mittel	hoch	Inland	true
11	Neukunde	mittel	hoch	Ausland	true
12	Stammkunde	mittel	niedrig	Ausland	true
13	Stammkunde	niedrig	hoch	Inland	true
14	Normalkunde	mittel	niedrig	Ausland	false

Gleich vorweg ein Disclaimer: Der Datensatz ist natürlich überaus klein, ja gerade zu winzig. Dafür würden wir in der Praxis niemals einen Machine Learning Algorithmus einsetzen. Dennoch bleiben wir besser übersichtlich und nachvollziehbar mit diesen 14 Zeilen. Das Lernziel dieser Übung ist es, ein Gefühl für die Erstellung von Entscheidungsbäumen zu erhalten.
Zu beachten ist ferner, dass dieser Datensatz bereits aggregiert ist, denn eigentlich nummerisch abbildbare Daten wurden in Klassen zusammengefasst.

Das Ziel:

Der Datensatz spielt wieder, welchem Kunden (ID) bisher die Zahlung per Rechnung erlaubt und nicht widerrufen wurde. Das Ziel soll sein, eine Vorhersage darüber zu machen zu können, wann ein Kunde per Rechnung zahlen darf und wann nicht (dann per Vorkasse).

Der Algorithmus:

Wir verwenden den ID3-Algorithmus in seiner Reinform. Der ID3-Algorithmus ist der gängigste Algorithmus zum Aufbau datengetriebener Entscheidungsbäume und es gibt mehrere Abwandlungen. Die Vorgehensweise des Algorithmus wird in dem Teil 2 der Artikelserie Entscheidungsbaum-Algorithmus ID3 erläutert.

1. Schritt: Auswählen des Attributes mit dem höchsten Informationsgewinn

Der Informationsgewinn eines Attributes ( $A$ ) im Sinne des ID3-Algorithmus ist die Differenz aus der Entropie ( $E(S)$ ) (siehe Teil 1 der Artikelserie Entropie, ein Maß für die Unreinheit in Daten) des gesamten Datensatzes ( $S$ ) und der Summe aus den gewichteten Entropien des Attributes für jeden einzelnen Wert (Value $i$ ), der im Attribut vorkommt:
$IG(S, A) = H(S) - \sum_{i=1}^n \frac{\bigl|S_i\bigl|}{\bigl|S\bigl|} \cdot H(S_i)$

1.1 Gesamt-Entropie des Datensatzes berechnen

Erstmal schauen wir uns die Entropie des gesamten Datensatzes an. Die Entropie bezieht sich dabei auf das gewünschte Klassifikationsergebnis, also ist die Zahlung via Rechnung erlaubt oder nicht? Diese Frage wird entweder mit true oder false beantwortet.

$H(S) = - \frac{9}{14} \cdot \log_2(\frac{9}{14}) - \frac{5}{14} \cdot \log_2(\frac{5}{14}) = 0.94$

1.2 Berechnung der Informationsgewinne aller Attribute

Berechnen wir nun also die Informationsgewinne über alle Spalten.

Attribut	Subset	Count(true)	Count(false)
Kundenart	“Neukunde”	2	3
	“Stammkunde”	4	0
	“Normalkunde”	3	2

Wir zerlegen den gesamten Datensatz gedanklich in drei Kategorien der Kundenart und berechnen die Entropie bezogen auf das Klassifikationsziel:

$H(S_{Neukunde}) = - \frac{2}{5} \cdot \log_2(\frac{2}{5}) - \frac{3}{5} \cdot \log_2(\frac{3}{5}) = 0.97$

$H(S_{Stammkunde}) = - \frac{4}{4} \cdot \log_2(\frac{4}{4}) - \frac{0}{4} \cdot \log_2(\frac{0}{4}) = 0.00$

$H(S_{Normalkunde}) = - \frac{3}{5} \cdot \log_2(\frac{3}{5}) - \frac{2}{5} \cdot \log_2(\frac{2}{5}) = 0.97$

Zur Erinnerung, der Informationsgewinn (Information Gain) wird wie folgt berechnet:

$IG(S, A_{Kundenart}) = - \sum_{i=1}^n \frac{\bigl|S_i\bigl|}{\bigl|S\bigl|} \cdot H(S_i)$

Angewendet auf das Attribut “Kundenart”…

$IG(S, A_{Kundenart}) = H(S) - \frac{\bigl|S_{Neukunde}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Neukunde}) - \frac{\bigl|S_{Stammkunde}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Stammkunde}) - \frac{\bigl|S_{Normalkunde}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Normalkunde})$

… erhalten wir der Formal nach folgenden Informationsgewinn:

$IG(S, A_{Kundenart}) = 0.94 - \frac{5}{14} \cdot 0.97 - \frac{4}{14} \cdot 0.00 - \frac{5}{14} \cdot 0.97 = 0.247$

Nun für die weiteren Spalten:

Attribut	Subset	Count(true)	Count(false)
Zahlungsgeschwindigkeit	“niedrig”	2	2
	“mittel”	4	2
	“schnell”	3	1

Entropien für die “Zahlungsgeschwindigkeit”:

$H(S_{niedrig}) = - \frac{2}{4} \cdot \log_2(\frac{2}{4}) - \frac{2}{4} \cdot \log_2(\frac{2}{4}) = 1.00$

$H(S_{mittel}) = - \frac{4}{6} \cdot \log_2(\frac{4}{6}) - \frac{2}{6} \cdot \log_2(\frac{2}{6}) = 0.92$

$H(S_{schnell}) = - \frac{3}{4} \cdot \log_2(\frac{3}{4}) - \frac{1}{4} \cdot \log_2(\frac{1}{4}) = 0.81$

So berechnen wir wieder den Informationsgewinn:

$IG(S, A_{Zahlungsgeschwindigkeit}) = H(S) - \frac{\bigl|S_{niedrig}\bigl|}{\bigl|S\bigl|} \cdot H(S_{niedrig}) - \frac{\bigl|S_{mittel}\bigl|}{\bigl|S\bigl|} \cdot H(S_{mittel}) - \frac{\bigl|S_{schnell}\bigl|}{\bigl|S\bigl|} \cdot H(S_{schnell})$

Einsatzen und ausrechnen:

$IG(S, A_{Zahlungsgeschwindigkeit}) = 0.94 - \frac{4}{14} \cdot 1.00 - \frac{6}{14} \cdot 0.92 - \frac{4}{14} \cdot 0.81 = 0.029$

Und nun für die Spalte “Kauffrequenz”:

Attribut	Subset	Count(true)	Count(false)
Kauffrequenz	“niedrig”	3	4
Kauffrequenz	“hoch”	6	1

Entropien:

$H(S_{niedrig}) = - \frac{3}{7} \cdot \log_2(\frac{3}{7}) - \frac{4}{7} \cdot \log_2(\frac{4}{7}) = 0.99$

$H(S_{hoch}) = - \frac{6}{7} \cdot \log_2(\frac{6}{7}) - \frac{1}{7} \cdot \log_2(\frac{1}{7}) = 0.59$

Informationsgewinn:

$IG(S, A_{Kauffrequenz}) = H(S) - \frac{\bigl|S_{niedrig}\bigl|}{\bigl|S\bigl|} \cdot H(S_{niedrig}) - \frac{\bigl|S_{hoch}\bigl|}{\bigl|S\bigl|} \cdot H(S_{hoch})$

Einsetzen und Ausrechnen:

$IG(S, A_{Kauffrequenz}) = 0.94 - \frac{7}{14} \cdot 1.00 - \frac{7}{14} \cdot 0.59 = 0.150$

Und last but not least die Spalte “Herkunft”:

Attribut	Subset	Count(true)	Count(false)
Herkunft	“Inland”	6	2
Herkunft	“Ausland”	3	3

Entropien:

$H(S_{Inland}) = - \frac{6}{8} \cdot \log_2(\frac{6}{8}) - \frac{2}{8} \cdot \log_2(\frac{2}{8}) = 0.81$

$H(S_{Ausland}) = - \frac{3}{6} \cdot \log_2(\frac{3}{6}) - \frac{3}{6} \cdot \log_2(\frac{3}{6}) = 1.00$

Informationsgewinn:

$IG(S, A_{Herkunft}) = H(S) - \frac{\bigl|S_{Inland}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Inland}) - \frac{\bigl|S_{Ausland}\bigl|}{\bigl|S\bigl|} \cdot H(S_{Ausland})$

Einsetzen und Ausrechnen:

$IG(S, A_{Herkunft}) = 0.94 - \frac{8}{14} \cdot 0.81 - \frac{6}{14} \cdot 1.00 = 0.05$

2. Schritt: Anlegen des Wurzel-Knotens

Der Informationsgewinn ist für das Attribut “Kundenart” am größten, daher entscheiden wir uns im Sinne des ID3-Algorithmus für dieses Attribut als Wurzel-Knoten.

3. Schritt: Rekursive Wiederholung (!!!)

Nun stellt sich natürlich die Frage: Wie geht es weiter?

Der Algorithmus kann eigentlich nur eines: Einen Wurzelknoten finden. Diesen Vorgang müssen wir nun nur noch rekursiv wiederholen, und das tun wir wie folgt.

Der Datensatz wurde bereits aufgeteilt in die drei Kundenarten. Für jede Kundenart ergibt sich jeweils ein Subset mit den verbleibenden Attributen. Für alle drei Subsets erstellen wir dann wieder einen Wurzelknoten, so dass ein neuer Ast entsteht.

3.1 Erster Rekursionsschritt

Machen wir also weiter und bestimmen wir das nächste Attribut nach der Kundenart, für die Fälle Kundenart = “Neukunde”:

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
1	Neukunde	niedrig	niedrig	Inland	false
2	Neukunde	niedrig	niedrig	Ausland	false
8	Neukunde	mittel	niedrig	Inland	false
9	Neukunde	hoch	hoch	Inland	true
11	Neukunde	mittel	hoch	Ausland	true

Die Entropie des Gesamtdatensatzes (ja, es ist für diesen Schritt betrachtet der gesamte Datensatz!) ist wie folgt:

$H(S_{Neukunde}) = - \frac{2}{5} \cdot \log_2(\frac{2}{5}) - \frac{3}{5} \cdot \log_2(\frac{3}{5}) = 0.97$

Die Entropie ist weit weg von einer bestimmten Wahrscheinlichkeit (nahe der Gleichverteilung). Daher müssen wir hier nochmal ansetzen und losrechnen:

Entropien für “Zahlungsgeschwindigkeit” bei Neukunden:

$H(S_{niedrig}) = 0.00$

$H(S_{mittel}) = 1.00$

$H(S_{hoch}) = 0.00$

Informationsgewinn des Attributes “Zahlungsgeschwindigkeit” bei Neukunden:

$IG(S_{Neukunde},A_{Zahlungsgeschwindigkeit}) = 0.97 - \frac{3}{5} \cdot 0.00 - \frac{2}{5} \cdot 1.00 - \frac{1}{5} \cdot 0.00 = 0.57$

Betrachtung der Spalte “Kauffrequenz” bei Neukunden:

Entropien für “Kauffrequenz” bei Neukunden:

$H(S_{niedrig}) = 0.00$

$H(S_{hoch}) = 0.00$

Informationsgewinn des Attributes “Kauffrequenz” bei Neukunden:

$IG(S_{Neukunde},A_{Kauffrequenz}) = 0.97 - \frac{3}{5} \cdot 0.00 - \frac{2}{5} \cdot 0.00 = 0.97$

Betrachtung der Spalte “Herkunft” bei Neukunden:

Entropien für “Herkunft” bei Neukunden:

$H(S_{Inland}) = 0.92$

$H(S_{hoch}) = 1.00$

Informationsgewinn des Attributes “Herkunft” bei Neukunden:

$IG(S_{Neukunde},A_{Herkunft}) = 0.97 - \frac{3}{5} \cdot 0.92 - \frac{2}{5} \cdot 1.00 = 0.018$

Wir entscheiden uns also für das Attribut “Kauffrequenz” als Ast nach der Entscheidung “Neukunde”, denn dieses Attribut bring uns den größten Informationsgewinn und trennt uns die Unterscheidung für oder gegen das Zahlungsmittel “Rechnung” eindeutig auf.

3.1 Zweiter Rekursionsschritt

Was passiert mit der Kundenart “Stammkunde”?

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
3	Stammkunde	niedrig	niedrig	Inland	true
7	Stammkunde	hoch	hoch	Ausland	true
12	Stammkunde	mittel	niedrig	Ausland	true
13	Stammkunde	niedrig	hoch	Inland	true

Die Antwort ist einfach: Nichts!
Wer ein Stammkunde ist, dem wurde stets die Zahlung per Rechnung erlaubt.

$H(S_{Stammkunde}) = 0.0$

3.1 Dritter Rekursionsschritt

Fehlt nun nur noch die Frage nach der Unterscheidung von Normalkunden.

Zeile	Kundenart	Zahlungsgeschwindigkeit	Kauffrequenz	Herkunft	Zahlungsmittel: Rechnung?
4	Normalkunde	mittel	niedrig	Inland	true
5	Normalkunde	hoch	hoch	Inland	true
6	Normalkunde	hoch	hoch	Ausland	false
14	Normalkunde	mittel	niedrig	Ausland	false

Zwar ist die Entropie des Subsets der Normalkunden…

$H(S_{Normalkunde}) = 1.0$

… denkbar schlecht, da maximal. Aber wir können genauso vorgehen, wie wir es bei dem Subset der Neukunden getan haben. Ich nehme es nun aber vorweg: Wenn wir uns den Datensatz näher ansehen, erkennen wir, dass wir diese Gesamtentropie von 1.0 für das Subset “Normalkunde” nicht mit den Attributen “Kauffrequenz” oder “Zahlungsgeschwindigkeit” reduzieren können, da dieses auch für sich betrachtet in Entropien der Größe 1.0 erhalten werden. Das Attribut “Herkunft” hingegen teilt den Datensatz sauber in true und false auf:

Somit ist der Informationsgewinn für das Attribut “Herkunft” am größten und wir haben unseren Baum komplett und – glücklicherweise – eindeutig bestimmen können!

Ergebnis: Der Entscheidungsbaum

Somit haben wir den Entscheidungsbaum über den ID3-Algorithmus erstellt, der eine Auskunft darüber macht, ob einem Kunden die Zahlung über Rechnung (statt Vorkasse) erlaubt wird:

true = Rechnung als Zahlungsmittel erlaubt
false = Rechnung als Zahlungsmittel nicht erlaubt

Ensemble Learning

December 3, 2017/1 Comment/in Artificial Intelligence, Big Data, Business Analytics, Data Mining, Data Science, Deep Learning, Machine Learning, Main Category /by Benjamin Aunkofer

Stellen Sie sich vor, Sie haben die Frage Ihres Lebens vor sich. Die korrekte Beantwortung dieser Frage wird Ihr Leben positiv beeinflussen, andernfalls negativ. Aber Sie haben Glück: Sie dürfen einen Experten, den Sie auswählen dürfen, um Rat fragen oder Sie dürfen eine annonyme Gruppe, sagen wir 1.000 Personen, um Rat fragen. Welchen Rat würden Sie sich einholen? Die einzelne Experten-Meinung oder die aggriegierte Antwort einer ganzen Gruppe von Menschen?
Oder wie wäre es mit einer Gruppe von Experten?

Ensemble Learning

Beim Einsatz eines maschinellen Lernalgorithmus auf ein bestimmtes Problem kann durchaus eine angemessene Präzision (Accuracy, eine Quote an Prädiktionsergebnissen, die als korrekt einzustufen sind) erzielt werden, doch oftmals reicht die Verlässlichkeit eines einzelnen Algorithmus nicht aus. Algorithmen können mit unterschiedlichen Parametern verwendet werden, die sich bei bestimmten Daten-Situationen verschieden auswirken. Bestimmte Algorithmen neigen zur Unteranpassung (Underfitting), andere zur Überanpassung (Overfitting).

Soll Machine Learning für den produktiven Einsatz mit bestmöglicher Zuverlässigkeit entwickelt und eingesetzt werden, kommt sinnvollerweise Ensemble Learning zum Einsatz. Beim Ensemble Learning wird ein Ensemble (Kollektiv von Prädiktoren) gebildet um ein Ensemble Average (Kollektivmittelwert) zu bilden. Sollte also beispielsweise einige Klassifizierer bei bestimmten Daten-Eingaben in ihren Ergebnissen ausreißen, steuern andere Klassifizierer dagegen. Ensemble Learning kommt somit in der Hoffnung zum Einsatz, dass eine Gruppe von Algorithmen ein besseres Ergebnis im Mittel erzeugen als es ein einzelner Algorithmus könnte.

Ich spreche nachfolgend bevorzugt von Klassifizierern, jedoch kommt Ensemble Learning auch bei der Regression zum Einsatz.

Voting Classifiers (bzw. Voting Regressors)

Eine häufige Form – und i.d.R. auch als erstes Beispiel eines Ensemble Learners – ist das Prinzip der Voting Classifiers. Das Prinzip der Voting Classifiers ist eine äußerst leicht nachvollziehbare Idee des Ensemble Learnings und daher vermutlich auch eine der bekanntesten Form der Kollektivmittelwert-Bildung. Gleich vorweg: Ja, es gibt auch Voting Regressors, jedoch ist dies ein Konzept, das nicht ganz ohne umfassendere Aggregation auf oberster Ebene auskommen wird, daher wäre für die Zwecke der akkurateren Regression eher das Stacking (siehe unten) sinnvoll.

Eine häufige Frage im Data Science ist, welcher Klassifizierer für bestimmte Zwecke die besseren sind: Entscheidungsbäume, Support-Vector-Machines, k-nächste-Nachbarn oder logistische Regressionen?

Warum nicht einfach alle nutzen? In der Tat wird genau das nicht selten praktiziert. Das Ziel dieser Form des Ensemble Learnings ist leicht zu erkennen: Die unterschiedlichen Schwächen aller Algorithmen sollen sich – so die Hoffnung – gegenseitig aufheben. Alle Algorithmen (dabei können auch mehrere gleiche Algorithmen mit jedoch jeweils unterschiedlichen Paramtern gemeint sein, z. B. mehrere knN-Klassifizierer mit unterschiedlichen k-Werten und Dimensionsgewichtungen) werden auf dasselbe Problem hin trainiert.

Bei der Prädiktion werden entweder alle Klassifizierer gleich behandelt oder unterschiedlich gewichtet (wobei größere Unterschiede der Gewichtungen unüblich, und vermutlich auch nicht sinnvoll, sind). Entsprechend einer Ensemble-Regel werden die Ergebnisse aller Klassifizierer aggregiert, bei Klassifikation durch eine Mehrheitsentscheidung, bei Regression meistens durch Durchschnittsbildung oder (beim Stacking) durch einen weiteren Regressor.

Abgesehen davon, dass wir mit dem Ensemble-Klassifizierer bzw. Regressoren vermutlich bessere Ergebnisse haben werden, haben wir nun auch eine weitere Information hinzubekommen: Eine Entropie über die Wahrscheinlichkeit. Bestenfalls haben alle Klassifizierer die gleiche Vorhersage berechnet, schlechtestensfalls haben wir ein Unentschieden. So können wir Vorhersagen in ihrer Aussagekraft bewerten. Analog kann bei Regressionen die Varianz der Ergebnisse herangezogen werden, um das Ergebnis in seiner Aussagekraft zu bewerten.

Betrachtung im Kontext von: Eine Kette ist nur so stark, wie ihr schwächstes Glied

Oft heißt es, dass Ensemble Learning zwar bessere Ergebnisse hervorbringt, als der schwächste Klassifizier in der Gruppe, aber auch schlechtere als der beste Klassifizierer. Ist Ensemble Learning also nur ein Akt der Ratlosigkeit, welcher Klassifizierer eigentlich der bessere wäre?

Ja und nein. Ensemble Learning wird tatsächlich in der Praxis dazu verwendet, einzelne Schwächen abzufangen und auch Ausreißer-Verhalten auf bisher andersartiger Daten abzuschwächen. Es ist ferner jedoch so, dass Ensemble Learner mit vielen Klassifizieren sogar bessere Vorhersagen liefern kann, als der beste Klassifizierer im Programm.

Das liegt an dem Gesetz der großen Zahlen, dass anhand eines Beispiels verdeutlicht werden kann: Bei einem (ausbalanzierten) Münzwurf liegt die Wahrscheinlichkeit bei genau 50,00% dafür, Kopf oder Zahl zu erhalten. Werfe ich die Münze beispielsweise zehn Mal, erhalte ich aber vielleicht drei Mal Kopf und sieben mal Zahl. Werfe ich sie 100 Mal, erhalte ich vielleicht 61 Mal Kopf und 39 Mal Zahl. Selbst nur 20 Mal die Zahl zu erhalten, wäre bei nur 100 Würfen gar nicht weit weg von unwahrscheinlich. Würde ich die Münze jedoch 10.000 Male werfen, würde ich den 50% schon sehr annähern, bei 10 Millionen Würfen wird sich die Verteilung ganz sicher als Gleichverteilung mit 50,0x% für Kopf oder Zahl einpendeln.

Nun stellt man sich (etwas überspitzt, da analog zu den Wünzwürfen) nun einen Ensemble Learner mit einer Gruppe von 10.000 Klassifiziern vor. Und angenommen, jeder einzelne Klassifizierer ist enorm schwach, denn eine richtige Vorhersage trifft nur mit einer Präzision von 51% zu (also kaum mehr als Glücksspiel), dann würde jedoch die Mehrheit der 10.000 Klassifizierer (nämlich 51%) richtig liegen und die Mehrheitsentscheidung in den absolut überwiegenden Fällen die korrekte Vorhersage treffen.

Was hingehen in diesem Kontext zutrifft: Prädiktionen via Ensemble Learning sind zwangsläufig langsam. Durch Parallelisierung der Klassifikation kann natürlich viel Zeit eingespart werden, dann ist das Ensemble Learning jedoch mindestens immer noch so langsam, wie der langsamste Klassifizierer.

Bagging

Ein Argument gegen den Einsatz von gänzlich verschiedenen Algortihmen ist, dass ein solcher Ensemble Learner nur schwer zu verstehen und einzuschätzen ist (übrigens ein generelles Problem im maschinellen Lernen). Bereits ein einzelner Algorithmus (z. B. Support Vector Machine) kann nach jedem Training alleine auf Basis der jeweils ausgewählten Daten (zum Training und zum Testen) recht unterschiedlich in seiner Vorhersage ausfallen.

Bagging (kurze Form von Bootstrap Aggregation) ist ein Ensemble Learning Prinzip, bei dem grundsätzlich der gleiche Algorithmus parallel mit unterschiedlichen Aufteilungen der Daten trainiert (und natürlich getestet) wird. Die Aufteilung der Daten kann dabei komplett (der vollständige Datensatz wird verteilt und verwendet) oder auch nur über Stichproben erfolgen (dann gibt es mehrfach verwendete Datenpunkte, aber auch solche, die überhaupt nicht verwendet werden). Das Ziel ist dabei insbesondere, im Endergebnis Unter- und Überanpassung zu vermeiden. Gibt es viele Dichte-Cluster und Ausreißer in den Daten, wird nicht jeder Klassifizierer sich diesen angepasst haben können. Jede Instanz der Klassifizierer erhält weitgehend unterschiedliche Daten mit eigenen Ausreißern und Dichte-Clustern, dabei darf es durchaus Überschneidungen bei der Datenaufteilung geben.

Pasting

Pasting ist fast genau wie Bagging, nur mit dem kleinen aber feinen Unterschied, dass sich die Datenaufteilung nicht überschneiden darf. Wird ein Datenpunkt durch Zufallsauswahl einem Klassifizierer zugewiesen, wird er nicht mehr für einen anderen Klassifizierer verwendet. Über die Trainingsdaten des einen Klassifizierers verfügt demnach kein anderer Klassifizierer. Die Klassifizierer sind somit völlig unabhängig voneinander trainiert, was manchmal explizit gewollt sein kann. Pasting setzt natürlich voraus, dass genug Daten vorhanden sind. Diese Voraussetzung ist gleichermaßen auch eine Antwort auf viele Probleme: Wie können große Datenmengen schnell verarbeitet werden? Durch die Aufteilung ohne Überschneidung auf parallele Knoten.

Random Forest

Random Forests sollten an dieser Stelle im Text eigentlich nicht stehen, denn sie sind ein Beispiel des parallelen Ensembles bzw. des Voting Classifiers mit Entscheidungsbäumen (Decision Trees). Random Forests möchte ich an dieser Stelle dennoch ansprechen, denn sie sind eine äußerst gängige Anwendung des Baggings oder (seltener) auch des Pastings für Entscheidungsbaumverfahren. Die Datenmenge wird durch Zufall aufgeteilt und aus jeder Aufteilung heraus wird ein Entscheidungsbaum erstellt. Eine Mehrheitsentscheidung der Klassifikationen aller Bäume ist das Ensemble Learning des Random Forests.

Random Forest ist ein Verfahren der Klassifikation oder Regression, das bereits so üblich ist, dass es mittlerweile längst in (fast) allen Machine Learning Bibliotheken implemeniert ist und – dank dieser Implementierung – in der Anwendung nicht komplizierter, als ein einzelner Entscheidungsbaum.

Stacking

Stacking ist eine Erweiterung des Voting Classifiers oder Voting Regressors um eine höhere Ebene (Blending-Level), die die beste Aggregation der Einzel-Ergebnisse erlernt. An der Spitze steht beim Stacking (mindestens) ein weiterer Klassifikator oder Regressor

Stacking ist insbesondere dann sinnvoll, wenn die Ergebnisse der einzelnen Algorithmen sehr unterschiedlich ausfallen können, was bei der Regression – da stetige Werte statt wenige Klassen – nahezu immer der Fall ist. Stacking-Algorithmen können sogar mehrere Schichten umfassen, was ihr Training wesentlich schwieriger gestaltet.

Boosting (Sequential Ensemble Learning)

Bagging, Pasting und Stacking sind parallele Verfahren des Ensemble Learning (was nicht bedeutet, dass die parallel dargestellten Algorithmen in der Praxis nicht doch sequenziell abgearbeitet werden). Zwangsweise sequenziell durchgeführt wird hingegen das Boosting, bei dem wir schwache Klassifizierer bzw. Regressoren durch Iteration in ihrem Training verstärken wollen. Boosting kann somit als eine Alternative zum Deep Learning gesehen werden. Während beim Deep Learning ein starker Algorithmus durch ein mehrschichtiges künstliches neuronales Netz dafür entworfen und trainiert wird, um ein komplexes Problem zu lösen (beispielsweise Testerkennung [OCR]), können derartige Herausforderungen auch mit schwächeren Klassifikatoren unter Einsatz von Boosting realisiert werden.

Boosting bezieht sich allein auf das Training und ist aus einer Not heraus entstanden: Wie bekommen wir bessere Prädiktionen mit einem eigentlich schwachen Lernalgorithmus, der tendenziell Unteranpassung erzeugt? Boosting ist eine Antwort auf Herausforderungen der Klassifikation oder Regression, bei der ein Algorithmus iterativ, also in mehreren Durchläufen, durch Anpassung von Gewichten trainiert wird.

Eines der bekanntesten Boosting-Verfahren ist AdaBoost. Der erste Schritt ist ein normales Training. Beim darauffolgenden Testen zeigen sich Klassifikations-/Regressionsfehler. Die fehlerhaft vorhergesagten Datenpunkte werden dann für einen nächsten Durchlauf höher gewichtet. Diese Iteration läuft einige Male, bis die Fehlerquote sich nicht mehr verbessert.

Bei AdaBoost werden falsch vorhergesagte Datensätze im jeweils nächsten Durchlauf höher gewichtet. Bei einem alternativen Boosing-Verfahren, dem Gradient Boosting (auf Basis der Gradientenmethode), werden Gewichtungen explizit in Gegenrichtung des Prädiktionsfehlers angepasst.

Was beispielsweise beim Voting Classifier der Random Forest ist, bei dem mehrere Entscheidungsbäume parallel arbeiten, sind das Äquvivalent beim Boosting die Gradient Boosted Trees, bei denen jeder Baum nur einen Teil der Daten akkurat beschreiben kann, die sequentielle Verschachtelung der Bäume jedoch auch herausfordernde Klassifikationen meistert.

Um bei dem Beispiel der Entscheidungsbäume zu bleiben: Sowohl Random Forests als auch Gradient Boosted Trees arbeiten grundsätzlich mit flachen Bäumen (schwache Klassifikatoren). Gradient Boosted Trees können durch die iterative Verstärkung generell eine höhere Präzision der Prädiktion erreichen als Random Forests, wenn die Feature- und Parameter-Auswahl bereits zu Anfang sinnvoll ist. Random Forests sind hingegen wiederum robuster bei der Feature- und Parameter-Auswahl, verstärken sich jedoch nicht gegenseitig, sondern sind in ihrem Endergebnis so gut, wie die Mehrheit der Bäume.

Buchempfehlungen

Mehr zum Thema Machine Learning und Ensemble Learning gewünscht? Folgende zwei Buchempfehlungen bieten nicht nur Erklärungen, sondern demonstrieren Ensemble Learning auch mit Beispiel-Code mit Python Scikit-Learn.


Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques for Building Intelligent Systems	Machine Learning mit Python: Das Praxis-Handbuch für Data Science, Predictive Analytics und Deep Learning (mitp Professional)