Introducing Google Brains‘ TensorFlow™
This week started with major news for the machine learning and data science community: the Google Brain Team announced the open sourcing of TensorFlow, their numerical library for tensor network computations. This software is actively developed (and used!) within Google and builds on many of Google’s large scale neural network applications such as automatic image labeling and captioning as well as the speech recognition in Google’s apps.

TensorFlow in bullet points
Here are the main features:
- Supports deep neural networks – and much more machine learning approaches
- Highly scalable across many machines and huge data sets
- Runs on desktops, servers, in cloud and even mobile devices
- Computation can run on CPUs, GPUs or both
- All this flexibility is covered by a single API making the execution very streamlined
- Available interfaces: C++ and Python. More will follow (Java, R, Lua, Go…)
- Comes with many tools helping to build and visualize the data flow networks
- Includes a powerful gradient based optimizer with auto-differentiation
- Extensible with C++
- Usable for commercial applications – released under Apache Software Licence 2.0
Tensor, what? Tensor, why?
„Numerical library for tensor network computations“ maybe doesn’t sound too exciting, but let’s consider the implications.
Application of tensors and their networks is a relatively new (but fast evolving) approach in machine learning. Tensors, if you recall your algebra classes, are simply n-dimensional data arrays (so a scalar is a 0th order tensor, a vector is 1st order, and a matrix a 2nd order matrix).
A simple practical example of is color image’s RGB layers (essentially three 2D matrices combined into a 3rd order tensor). Or a more business minded example – if your data source generates a table (a 2D array) every hour, you can look at the full data set as a 3rd order tensor – time being the extra dimension.
Tensor networks then represent “data flow graphs”, where the edges are your multi-dimensional data sets and nodes are the mathematical operations on this data.
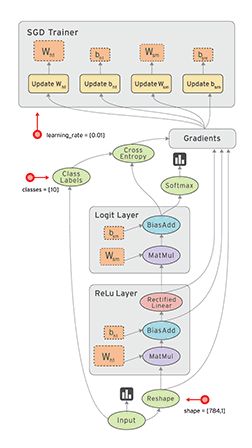 gif
gifExample of of a data flow graph with multiple nodes (data operations). Notice how the execution of nodes is asynchronous. This allows incredible scalability across many machines. Image Source.
Looking at your data through the tensor formalism gives you a lot of powerful tools that were already developed for tensor algebra, allowing fast, complex computations.
Tensor networks are also a natural fit for computations done on graphical processing units (GPUs) as they are built exactly for the purpose of very fast numerical operations on such a data – speeding up your calculations significantly compared to standard CPU execution!
The importance of flexible architecture & scaling
The data flow graph approach has also further advantages. Most notably, you can split the design of your data flows (i.e. data cleaning, processing, transformations, model building etc.) from its execution. You first build up the graph of your data flow and then you send it to for execution: either on the CPUs of your machines (and it can be your laptop just as well as cluster) or GPUs or a combination. This happens through a single interface that hides all the complexities from you.
Since the execution is asynchronous it scales across many machines and can deal with huge amounts of data.
You can count on the Google guys to build tools not only for academic use, but also heavy-duty operations in the industry!
Is this just another deep learning library?
TensorFlow is of course not the first library to embrace the tensor formalism and GPU execution. The nearest comparisons (and competitors) are Theano, Torch and CGT (Caffe to a limited degree).
While there are significant overlaps between the libraries, TensorFlow tries to provide a broader framework. It is not only a deep learning library – the Data Flow Graphs can incorporate any data processing/analysis applications. It also comes with a very powerful gradient based optimizer with automatic calculations of derivatives offering huge flexibility.
Given this broad vision the closest competitor is probably Theano (while Caffe and the existing Theano wrappers have a narrower focus on deep learning). TensorFlow’s distinguishing feature is that by design its focus is on large, scalable architectures with a complete flexibility in the hardware, best suited for industry/operational use, whereas the other libraries have more academic pedigrees.
Initial analyses also indicate that TensorFlow should bring also performance improvements compared to Theano, although no comprehensive benchmarks have yet been published.
As the other packages are out already for a while, they have large, active communities and often additional supporting software (examples are the very useful wrappers around Theano like Lasagne, Keras and Blocks that provider higher level abstractions to its engine).
Of course, with Google’s gravitas, one can expect that TensorFlow’s open source community will grow very fast and the contributors will quickly add a lot of additional features (and find hidden bugs).
Finally, keep in mind, that while Google provided us with this great data processing framework and some of its machine learning capabilities, it is likely that the most powerful machine learning algorithms still remain Google’s proprietary secret.
Nonetheless, TensorFlow is a huge and very welcome contribution to the open source machine learning world!
Where to go next?
You can find Google’s getting started guide here. The TensorFlow white paper is worth a read too. Source code can be found at the Github page. There is also a Vagrant virtual machine with TensorFlow pre-installed available here.






 gif
gif